Tetrahedrons - PSAT Math
Card 0 of 42
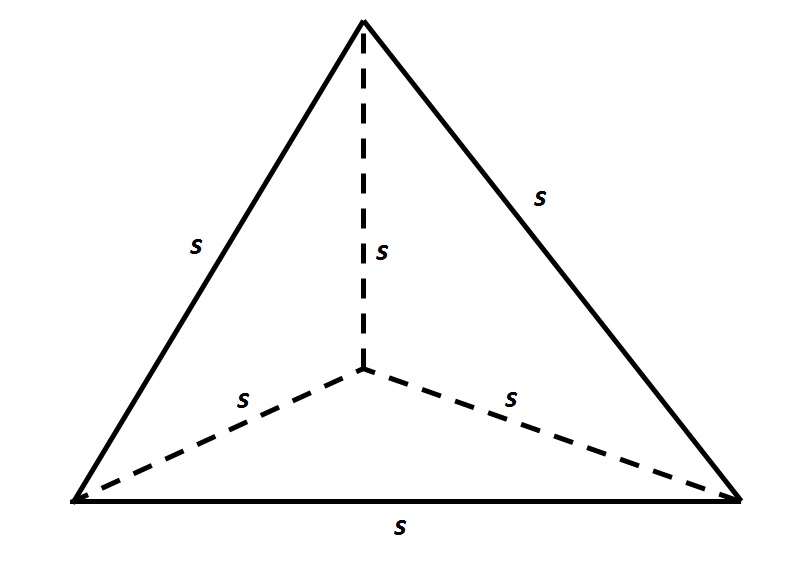
Refer to the above tetrahedron, or four-faced solid.The surface area of the tetrahedron is 444. Evaluate  to the nearest tenth.
to the nearest tenth.

Refer to the above tetrahedron, or four-faced solid.The surface area of the tetrahedron is 444. Evaluate 
Tap to see back →
The tetrahedron has four faces, each of which is an equilateral triangle with sidelength  . Since the total surface area is 444, each triangle has area one fourth of this, or 111. To find
. Since the total surface area is 444, each triangle has area one fourth of this, or 111. To find  , set
, set 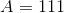 in the formula for the area of an equilateral triangle:
in the formula for the area of an equilateral triangle:
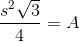

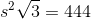

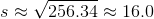
The tetrahedron has four faces, each of which is an equilateral triangle with sidelength 

A regular tetrahedron has four congruent faces, each of which is an equilateral triangle.
A given tetrahedron has edges of length six inches. Give the total surface area of the tetrahedron.
A regular tetrahedron has four congruent faces, each of which is an equilateral triangle.
A given tetrahedron has edges of length six inches. Give the total surface area of the tetrahedron.
Tap to see back →
The area of an equilateral triangle is given by the formula

Since there are four equilateral triangles that comprise the surface of the tetrahedron, the total surface area is

Substitute  :
:
 square inches.
square inches.
The area of an equilateral triangle is given by the formula
Since there are four equilateral triangles that comprise the surface of the tetrahedron, the total surface area is
Substitute 


Give the surface area of the above tetrahedron, or four-faced solid, to the nearest tenth.

Give the surface area of the above tetrahedron, or four-faced solid, to the nearest tenth.
Tap to see back →
The tetrahedron has four faces, each of which is an equilateral triangle with sidelength 7. Each face has area

The total surface area is four times this, or about  .
.
Rounded, this is 84.9.
The tetrahedron has four faces, each of which is an equilateral triangle with sidelength 7. Each face has area
The total surface area is four times this, or about 
Rounded, this is 84.9.

Note: Figure NOT drawn to scale.
The above triangular pyramid has volume 25. To the nearest tenth, evaluate  .
.

Note: Figure NOT drawn to scale.
The above triangular pyramid has volume 25. To the nearest tenth, evaluate 
Tap to see back →
We are looking for the height of the pyramid.
The base is an equilateral triangle with sidelength 4, so its area can be calculated as follows:




The height  of a pyramid can be calculated using the fomula
of a pyramid can be calculated using the fomula

We set  and
and  and solve for
and solve for  :
:


We are looking for the height of the pyramid.
The base is an equilateral triangle with sidelength 4, so its area can be calculated as follows:
The height 
We set 



Note: Figure NOT drawn to scale.
Give the volume (nearest tenth) of the above triangular pyramid.

Note: Figure NOT drawn to scale.
Give the volume (nearest tenth) of the above triangular pyramid.
Tap to see back →
The height of the pyramid is  . The base is an equilateral triangle with sidelength 4, so its area can be calculated as follows:
. The base is an equilateral triangle with sidelength 4, so its area can be calculated as follows:




The volume of a pyramid can be calculated using the fomula


The height of the pyramid is 
The volume of a pyramid can be calculated using the fomula
A regular tetrahedron has an edge length of  . What is its volume?
. What is its volume?
A regular tetrahedron has an edge length of 
Tap to see back →
The volume of a tetrahedron is found with the equation  , where
, where  represents the length of an edge of the tetrahedron.
represents the length of an edge of the tetrahedron.
Plug in 4 for the edge length and reduce as much as possible to find the answer:



The volume of the tetrahedron is  .
.
The volume of a tetrahedron is found with the equation 

Plug in 4 for the edge length and reduce as much as possible to find the answer:
The volume of the tetrahedron is 

Refer to the above tetrahedron, or four-faced solid.The surface area of the tetrahedron is 444. Evaluate  to the nearest tenth.
to the nearest tenth.

Refer to the above tetrahedron, or four-faced solid.The surface area of the tetrahedron is 444. Evaluate 
Tap to see back →
The tetrahedron has four faces, each of which is an equilateral triangle with sidelength  . Since the total surface area is 444, each triangle has area one fourth of this, or 111. To find
. Since the total surface area is 444, each triangle has area one fourth of this, or 111. To find  , set
, set 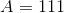 in the formula for the area of an equilateral triangle:
in the formula for the area of an equilateral triangle:

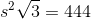

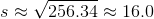
The tetrahedron has four faces, each of which is an equilateral triangle with sidelength 

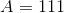
A regular tetrahedron has four congruent faces, each of which is an equilateral triangle.
A given tetrahedron has edges of length six inches. Give the total surface area of the tetrahedron.
A regular tetrahedron has four congruent faces, each of which is an equilateral triangle.
A given tetrahedron has edges of length six inches. Give the total surface area of the tetrahedron.
Tap to see back →
The area of an equilateral triangle is given by the formula

Since there are four equilateral triangles that comprise the surface of the tetrahedron, the total surface area is

Substitute  :
:
 square inches.
square inches.
The area of an equilateral triangle is given by the formula
Since there are four equilateral triangles that comprise the surface of the tetrahedron, the total surface area is
Substitute 


Give the surface area of the above tetrahedron, or four-faced solid, to the nearest tenth.

Give the surface area of the above tetrahedron, or four-faced solid, to the nearest tenth.
Tap to see back →
The tetrahedron has four faces, each of which is an equilateral triangle with sidelength 7. Each face has area

The total surface area is four times this, or about  .
.
Rounded, this is 84.9.
The tetrahedron has four faces, each of which is an equilateral triangle with sidelength 7. Each face has area
The total surface area is four times this, or about 
Rounded, this is 84.9.

Note: Figure NOT drawn to scale.
The above triangular pyramid has volume 25. To the nearest tenth, evaluate  .
.

Note: Figure NOT drawn to scale.
The above triangular pyramid has volume 25. To the nearest tenth, evaluate 
Tap to see back →
We are looking for the height of the pyramid.
The base is an equilateral triangle with sidelength 4, so its area can be calculated as follows:




The height  of a pyramid can be calculated using the fomula
of a pyramid can be calculated using the fomula

We set  and
and  and solve for
and solve for  :
:


We are looking for the height of the pyramid.
The base is an equilateral triangle with sidelength 4, so its area can be calculated as follows:
The height 
We set 



Note: Figure NOT drawn to scale.
Give the volume (nearest tenth) of the above triangular pyramid.

Note: Figure NOT drawn to scale.
Give the volume (nearest tenth) of the above triangular pyramid.
Tap to see back →
The height of the pyramid is  . The base is an equilateral triangle with sidelength 4, so its area can be calculated as follows:
. The base is an equilateral triangle with sidelength 4, so its area can be calculated as follows:




The volume of a pyramid can be calculated using the fomula


The height of the pyramid is 
The volume of a pyramid can be calculated using the fomula
A regular tetrahedron has an edge length of  . What is its volume?
. What is its volume?
A regular tetrahedron has an edge length of 
Tap to see back →
The volume of a tetrahedron is found with the equation  , where
, where  represents the length of an edge of the tetrahedron.
represents the length of an edge of the tetrahedron.
Plug in 4 for the edge length and reduce as much as possible to find the answer:



The volume of the tetrahedron is  .
.
The volume of a tetrahedron is found with the equation 

Plug in 4 for the edge length and reduce as much as possible to find the answer:
The volume of the tetrahedron is 

Refer to the above tetrahedron, or four-faced solid.The surface area of the tetrahedron is 444. Evaluate  to the nearest tenth.
to the nearest tenth.

Refer to the above tetrahedron, or four-faced solid.The surface area of the tetrahedron is 444. Evaluate 
Tap to see back →
The tetrahedron has four faces, each of which is an equilateral triangle with sidelength  . Since the total surface area is 444, each triangle has area one fourth of this, or 111. To find
. Since the total surface area is 444, each triangle has area one fourth of this, or 111. To find  , set
, set 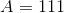 in the formula for the area of an equilateral triangle:
in the formula for the area of an equilateral triangle:
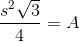

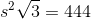

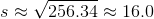
The tetrahedron has four faces, each of which is an equilateral triangle with sidelength 

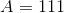
A regular tetrahedron has four congruent faces, each of which is an equilateral triangle.
A given tetrahedron has edges of length six inches. Give the total surface area of the tetrahedron.
A regular tetrahedron has four congruent faces, each of which is an equilateral triangle.
A given tetrahedron has edges of length six inches. Give the total surface area of the tetrahedron.
Tap to see back →
The area of an equilateral triangle is given by the formula

Since there are four equilateral triangles that comprise the surface of the tetrahedron, the total surface area is

Substitute  :
:
 square inches.
square inches.
The area of an equilateral triangle is given by the formula
Since there are four equilateral triangles that comprise the surface of the tetrahedron, the total surface area is
Substitute 


Give the surface area of the above tetrahedron, or four-faced solid, to the nearest tenth.

Give the surface area of the above tetrahedron, or four-faced solid, to the nearest tenth.
Tap to see back →
The tetrahedron has four faces, each of which is an equilateral triangle with sidelength 7. Each face has area

The total surface area is four times this, or about  .
.
Rounded, this is 84.9.
The tetrahedron has four faces, each of which is an equilateral triangle with sidelength 7. Each face has area
The total surface area is four times this, or about 
Rounded, this is 84.9.

Note: Figure NOT drawn to scale.
The above triangular pyramid has volume 25. To the nearest tenth, evaluate  .
.

Note: Figure NOT drawn to scale.
The above triangular pyramid has volume 25. To the nearest tenth, evaluate 
Tap to see back →
We are looking for the height of the pyramid.
The base is an equilateral triangle with sidelength 4, so its area can be calculated as follows:




The height  of a pyramid can be calculated using the fomula
of a pyramid can be calculated using the fomula

We set  and
and  and solve for
and solve for  :
:


We are looking for the height of the pyramid.
The base is an equilateral triangle with sidelength 4, so its area can be calculated as follows:
The height 
We set 



Note: Figure NOT drawn to scale.
Give the volume (nearest tenth) of the above triangular pyramid.

Note: Figure NOT drawn to scale.
Give the volume (nearest tenth) of the above triangular pyramid.
Tap to see back →
The height of the pyramid is  . The base is an equilateral triangle with sidelength 4, so its area can be calculated as follows:
. The base is an equilateral triangle with sidelength 4, so its area can be calculated as follows:




The volume of a pyramid can be calculated using the fomula


The height of the pyramid is 
The volume of a pyramid can be calculated using the fomula
A regular tetrahedron has an edge length of  . What is its volume?
. What is its volume?
A regular tetrahedron has an edge length of 
Tap to see back →
The volume of a tetrahedron is found with the equation  , where
, where  represents the length of an edge of the tetrahedron.
represents the length of an edge of the tetrahedron.
Plug in 4 for the edge length and reduce as much as possible to find the answer:



The volume of the tetrahedron is  .
.
The volume of a tetrahedron is found with the equation 

Plug in 4 for the edge length and reduce as much as possible to find the answer:
The volume of the tetrahedron is 

Refer to the above tetrahedron, or four-faced solid.The surface area of the tetrahedron is 444. Evaluate  to the nearest tenth.
to the nearest tenth.

Refer to the above tetrahedron, or four-faced solid.The surface area of the tetrahedron is 444. Evaluate 
Tap to see back →
The tetrahedron has four faces, each of which is an equilateral triangle with sidelength  . Since the total surface area is 444, each triangle has area one fourth of this, or 111. To find
. Since the total surface area is 444, each triangle has area one fourth of this, or 111. To find  , set
, set 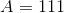 in the formula for the area of an equilateral triangle:
in the formula for the area of an equilateral triangle:
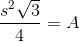

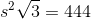

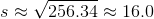
The tetrahedron has four faces, each of which is an equilateral triangle with sidelength 

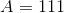
A regular tetrahedron has four congruent faces, each of which is an equilateral triangle.
A given tetrahedron has edges of length six inches. Give the total surface area of the tetrahedron.
A regular tetrahedron has four congruent faces, each of which is an equilateral triangle.
A given tetrahedron has edges of length six inches. Give the total surface area of the tetrahedron.
Tap to see back →
The area of an equilateral triangle is given by the formula

Since there are four equilateral triangles that comprise the surface of the tetrahedron, the total surface area is

Substitute  :
:
 square inches.
square inches.
The area of an equilateral triangle is given by the formula
Since there are four equilateral triangles that comprise the surface of the tetrahedron, the total surface area is
Substitute 
