Circles - SAT Math
Card 0 of 11
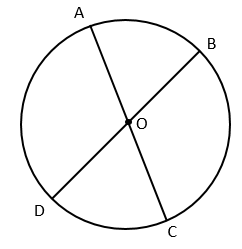
In the circle above, centered on point O, angle AOB measures 40 degrees. If line segment BD measures 18 inches, what is the measure, in inches, of minor arc BC?

In the circle above, centered on point O, angle AOB measures 40 degrees. If line segment BD measures 18 inches, what is the measure, in inches, of minor arc BC?
Tap to see back →
To calculate an arc length, you need: 1) The circumference of the circle (πd where d is the diameter), and 2) The measure of the central angle. Here the diameter is 18, so circumference is 18π. Angle BOC is 140 degrees (since AOB and BOC complete the 180-degree line AC). Therefore: 140/360 × 18π = 7/18 × 18π = 7π.
To calculate an arc length, you need: 1) The circumference of the circle (πd where d is the diameter), and 2) The measure of the central angle. Here the diameter is 18, so circumference is 18π. Angle BOC is 140 degrees (since AOB and BOC complete the 180-degree line AC). Therefore: 140/360 × 18π = 7/18 × 18π = 7π.
Equation of a circle with center $(h, k)$ and radius $r$.
Equation of a circle with center $(h, k)$ and radius $r$.
Tap to see back →
$(x - h)^2 + (y - k)^2 = r^2$.
$(x - h)^2 + (y - k)^2 = r^2$.
Formula for arc length.
Formula for arc length.
Tap to see back →
$s = \frac{\theta}{360^{\circ}} \times 2\pi r$.
$s = \frac{\theta}{360^{\circ}} \times 2\pi r$.
Formula for area of a circle.
Formula for area of a circle.
Tap to see back →
$A = \pi r^2$.
$A = \pi r^2$.
Formula for area of a sector.
Formula for area of a sector.
Tap to see back →
$A = \frac{\theta}{360^{\circ}} \times \pi r^2$.
$A = \frac{\theta}{360^{\circ}} \times \pi r^2$.
Define a chord.
Define a chord.
Tap to see back →
A segment connecting two points on the circle.
A segment connecting two points on the circle.
If a tangent and secant are drawn from a point outside a circle, relation between lengths.
If a tangent and secant are drawn from a point outside a circle, relation between lengths.
Tap to see back →
$t^2 = e(e + s)$, where $t$ is tangent, $e$ is external part of secant, $s$ is internal segment.
$t^2 = e(e + s)$, where $t$ is tangent, $e$ is external part of secant, $s$ is internal segment.
Relationship between a central angle and its intercepted arc.
Relationship between a central angle and its intercepted arc.
Tap to see back →
They have equal measures.
They have equal measures.
Relationship between radius and tangent.
Relationship between radius and tangent.
Tap to see back →
A radius is perpendicular to the tangent at the point of tangency.
A radius is perpendicular to the tangent at the point of tangency.
When is the solution of an inequality written with an open circle on a number line?
When is the solution of an inequality written with an open circle on a number line?
Tap to see back →
When the inequality is strict ($<$ or $>$).
When the inequality is strict ($<$ or $>$).
Formula for circumference of a circle.
Formula for circumference of a circle.
Tap to see back →
$C = 2\pi r$.
$C = 2\pi r$.