Solving Functions - SAT Math
Card 0 of 312
If  , what must
, what must  be?
be?
If 

Replace the value of negative two with the x-variable.
There is no need to use the FOIL method to expand the binomial.

The answer is: 
Replace the value of negative two with the x-variable.
There is no need to use the FOIL method to expand the binomial.
The answer is:
Compare your answer with the correct one above
Let  . What is the value of
. What is the value of  ?
?
Let 

Substitute the fraction as  .
.

Multiply the whole number with the numerator.

Convert the expression so that both terms have similar denominators.

The answer is: 
Substitute the fraction as 
Multiply the whole number with the numerator.
Convert the expression so that both terms have similar denominators.
The answer is:
Compare your answer with the correct one above
If  , what must
, what must  be?
be?
If 

A function of x equals five. This can be translated to:

This means that every point on the x-axis has a y value of five.
Therefore,  .
.
The answer is: 
A function of x equals five. This can be translated to:
This means that every point on the x-axis has a y value of five.
Therefore, 
The answer is:
Compare your answer with the correct one above
A baseball is thrown straight up with an initial speed of 60 feet per second by a man standing on the roof of a 100-foot high building. The height of the baseball in feet as a function of time  in seconds is modeled by the function
in seconds is modeled by the function

To the nearest tenth of a second, how long does it take for the baseball to hit the ground?
A baseball is thrown straight up with an initial speed of 60 feet per second by a man standing on the roof of a 100-foot high building. The height of the baseball in feet as a function of time 
To the nearest tenth of a second, how long does it take for the baseball to hit the ground?
When the baseball hits the ground, the height is 0, so we set  . and solve for
. and solve for 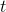 .
.

This can be done using the quadratic formula:

Set  :
:





One possible solution:

We throw this out, since time must be positive.
The other:

This solution, we keep. The baseball hits the ground in 5 seconds.
When the baseball hits the ground, the height is 0, so we set 
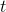
This can be done using the quadratic formula:
Set 
One possible solution:
We throw this out, since time must be positive.
The other:
This solution, we keep. The baseball hits the ground in 5 seconds.
Compare your answer with the correct one above
If  , what is the value of
, what is the value of  ?
?
If 

Substitute the value of negative three as 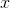 .
.


The terms will be imaginary. We can factor out an 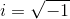 out of the right side. Replace them with
out of the right side. Replace them with  .
.
The answer is: 
Substitute the value of negative three as 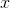
The terms will be imaginary. We can factor out an 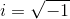

The answer is:
Compare your answer with the correct one above
What is the horizontal asymptote of the graph of the equation  ?
?
What is the horizontal asymptote of the graph of the equation 
The asymptote of this equation can be found by observing that  regardless of
regardless of  . We are thus solving for the value of
. We are thus solving for the value of  as
as  approaches zero.
approaches zero.





So the value that  cannot exceed is
cannot exceed is  , and the line
, and the line  is the asymptote.
is the asymptote.
The asymptote of this equation can be found by observing that 



So the value that 


Compare your answer with the correct one above
Solve the equation for  .
.

Solve the equation for 
Begin by recognizing that both sides of the equation have a root term of  .
.


Using the power rule, we can set the exponents equal to each other.



Begin by recognizing that both sides of the equation have a root term of 
Using the power rule, we can set the exponents equal to each other.
Compare your answer with the correct one above
Solve the equation for  .
.

Solve the equation for 
Begin by recognizing that both sides of the equation have the same root term,  .
.



We can use the power rule to combine exponents.

Set the exponents equal to each other.


Begin by recognizing that both sides of the equation have the same root term, 
We can use the power rule to combine exponents.
Set the exponents equal to each other.
Compare your answer with the correct one above
What is/are the asymptote(s) of the graph of the function
 ?
?
What is/are the asymptote(s) of the graph of the function

An exponential equation of the form  has only one asymptote - a horizontal one at
has only one asymptote - a horizontal one at  . In the given function,
. In the given function,  , so its one and only asymptote is
, so its one and only asymptote is  .
.
An exponential equation of the form 



Compare your answer with the correct one above
Find the vertical asymptote of the equation.

Find the vertical asymptote of the equation.
To find the vertical asymptotes, we set the denominator of the function equal to zero and solve.




To find the vertical asymptotes, we set the denominator of the function equal to zero and solve.
Compare your answer with the correct one above
In 2009, the population of fish in a pond was 1,034. In 2013, it was 1,711.
Write an exponential growth function of the form  that could be used to model
that could be used to model  , the population of fish, in terms of
, the population of fish, in terms of  , the number of years since 2009.
, the number of years since 2009.
In 2009, the population of fish in a pond was 1,034. In 2013, it was 1,711.
Write an exponential growth function of the form 


Solve for the values of a and b:
In 2009,  and
and  (zero years since 2009). Plug this into the exponential equation form:
(zero years since 2009). Plug this into the exponential equation form:
 . Solve for
. Solve for  to get
to get  .
.
In 2013,  and
and  . Therefore,
. Therefore,
 or
or  . Solve for
. Solve for  to get
to get
![b=\sqrt[4]{\frac{1711}{1034}}\approx1.1342](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/220698/gif.latex) .
.
Then the exponential growth function is
 .
.
Solve for the values of a and b:
In 2009, 




In 2013, 




![b=\sqrt[4]{\frac{1711}{1034}}\approx1.1342](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/220698/gif.latex)
Then the exponential growth function is

Compare your answer with the correct one above
Determine whether each function represents exponential decay or growth.


Determine whether each function represents exponential decay or growth.
a)
This is exponential decay since the base,  , is between
, is between  and
and  .
.
b)
This is exponential growth since the base,  , is greater than
, is greater than  .
.
a)
This is exponential decay since the base, 


b)
This is exponential growth since the base, 

Compare your answer with the correct one above

Solve for  .
.
Solve for 
8 and 4 are both powers of 2.



8 and 4 are both powers of 2.
Compare your answer with the correct one above
Give the  -intercept of the graph of the equation
-intercept of the graph of the equation  .
.
Give the 

Set  and solve for
and solve for 



We need not work further. It is impossible to raise a positive number 2 to any real power to obtain a negative number. Therefore, the equation has no solution, and the graph of  has no
has no  -intercept.
-intercept.
Set 
We need not work further. It is impossible to raise a positive number 2 to any real power to obtain a negative number. Therefore, the equation has no solution, and the graph of 

Compare your answer with the correct one above
What is/are the asymptote(s) of the graph of the function  ?
?
What is/are the asymptote(s) of the graph of the function 
An exponential function of the form

has as its one and only asymptote the horizontal line  .
.
Since we define  as
as
 ,
,
then  ,
,
and the only asymptote is the line of the equation  .
.
An exponential function of the form
has as its one and only asymptote the horizontal line 
Since we define 

then 
and the only asymptote is the line of the equation 
Compare your answer with the correct one above
Match each function with its graph.
1. 
2. 
3. 
a.
b.
c.
Match each function with its graph.
1.
2.
3.
a.
b.
c.
For  , our base is greater than
, our base is greater than  so we have exponential growth, meaning the function is increasing. Also, when
so we have exponential growth, meaning the function is increasing. Also, when  , we know that
, we know that  since
since  . The only graph that fits these conditions is
. The only graph that fits these conditions is  .
.
For  , we have exponential growth again but when
, we have exponential growth again but when  ,
,  . This is shown on graph
. This is shown on graph  .
.
For  , we have exponential decay so the graph must be decreasing. Also, when
, we have exponential decay so the graph must be decreasing. Also, when  ,
,  . This is shown on graph
. This is shown on graph  .
.
For 





For 



For 



Compare your answer with the correct one above
What is the  -intercept of
-intercept of  ?
?
What is the 

The  -intercept of a graph is the point on the graph where the
-intercept of a graph is the point on the graph where the  -value is
-value is  .
.
Thus, to find the  -intercept, substitute
-intercept, substitute  and solve for
and solve for  .
.
Thus, we get:

The 


Thus, to find the 


Thus, we get:
Compare your answer with the correct one above
In 2010, the population of trout in a lake was 416. It has increased to 521 in 2015.
Write an exponential function of the form  that could be used to model the fish population of the lake. Write the function in terms of
that could be used to model the fish population of the lake. Write the function in terms of  , the number of years since 2010.
, the number of years since 2010.
In 2010, the population of trout in a lake was 416. It has increased to 521 in 2015.
Write an exponential function of the form 

We need to determine the constants  and
and  . Since
. Since  in 2010 (when
in 2010 (when  ), then
), then  and
and 
To get  , we find that when
, we find that when  ,
,  . Then
. Then  .
.
Using a calculator,  , so
, so  .
.
Then our model equation for the fish population is 
We need to determine the constants 




To get 



Using a calculator, 

Then our model equation for the fish population is
Compare your answer with the correct one above
An exponential funtion  is graphed on the figure below to model some data that shows exponential decay. At
is graphed on the figure below to model some data that shows exponential decay. At  ,
,  is at half of its initial value (value when
is at half of its initial value (value when  ). Find the exponential equation of the form
). Find the exponential equation of the form  that fits the data in the graph, i.e. find the constants
that fits the data in the graph, i.e. find the constants  and
and  .
.

An exponential funtion 







To determine the constant  , we look at the graph to find the initial value of
, we look at the graph to find the initial value of  , (when
, (when  ) and find it to be
) and find it to be  . We can then plug this into our equation
. We can then plug this into our equation  and we get
and we get  . Since
. Since  , we find that
, we find that  .
.
To find  , we use the fact that when
, we use the fact that when  ,
,  is one half of the initial value
is one half of the initial value  . Plugging this into our equation with
. Plugging this into our equation with  now known gives us
now known gives us  . To solve for
. To solve for  , we make use the fact that the natural log is the inverse function of
, we make use the fact that the natural log is the inverse function of  , so that
, so that
 .
.
We can write our equation as  and take the natural log of both sides to get:
and take the natural log of both sides to get:
 or
or  .
.
Then  .
.
Our model equation is  .
.
To determine the constant 







To find 








We can write our equation as 


Then 
Our model equation is 
Compare your answer with the correct one above
Consider the exponential function  . Determine if there are any asymptotes and where they lie on the graph.
. Determine if there are any asymptotes and where they lie on the graph.
Consider the exponential function 
For positive  values,
values,  increases exponentially in the
increases exponentially in the  direction and goes to positive infinity, so there is no asymptote on the positive
direction and goes to positive infinity, so there is no asymptote on the positive  -axis. For negative
-axis. For negative  values, as
values, as  decreases, the term
decreases, the term  becomes closer and closer to zero so
becomes closer and closer to zero so  approaches
approaches  as we move along the negative
as we move along the negative  axis. As the graph below shows, this is forms a horizontal asymptote.
axis. As the graph below shows, this is forms a horizontal asymptote.

For positive 










Compare your answer with the correct one above