How to simplify square roots - SAT Math

Card 0 of 424

Question

Simplify

9 ÷ √3

Answer

in order to simplify a square root on the bottom, multiply top and bottom by the root

Compare your answer with the correct one above

Question

Simplify:

√112

Answer

√112 = {√2 * √56} = {√2 * √2 * √28} = {2√28} = {2√4 * √7} = 4√7

Compare your answer with the correct one above

Question

Simplify the following: (√(6) + √(3)) / √(3)

Answer

Begin by multiplying top and bottom by √(3):

(√(18) + √(9)) / 3

Note the following:

√(9) = 3

√(18) = √(9 * 2) = √(9) * √(2) = 3 * √(2)

Therefore, the numerator is: 3 * √(2) + 3. Factor out the common 3: 3 * (√(2) + 1)

Rewrite the whole fraction:

(3 * (√(2) + 1)) / 3

Simplfy by dividing cancelling the 3 common to numerator and denominator: √(2) + 1

Compare your answer with the correct one above

Question

Simplify:

√192

Answer

√192 = √2 X √96

√96 = √2 X √48

√48 = √4 X√12

√12 = √4 X √3

√192 = √(2X2X4X4) X √3

= √4X√4X√4 X √3

= 8√3

Compare your answer with the correct one above

Question

what is

√0.0000490

Answer

easiest way to simplify: turn into scientific notation

√0.0000490= √4.9 X 10-5

finding the square root of an even exponent is easy, and 49 is a perfect square, so we can write out an improper scientific notation:

√4.9 X 10-5 = √49 X 10-6

√49 = 7; √10-6 = 10-3 this is equivalent to raising 10-6 to the 1/2 power, in which case all that needs to be done is multiply the two exponents: 7 X 10-3= 0.007

Compare your answer with the correct one above

Question

Which of the following is the most simplified form of:

$\sqrt{468}$

Answer

First find all of the prime factors of

$468=6\ast78=6\ast6\ast13=2\ast3\ast2\ast3\ast13$

So $\sqrt{468}=\sqrt{2\ast2\ast3\ast3\ast13}=2\ast3\sqrt{13}=6\sqrt{13}$

Compare your answer with the correct one above

Question

Which of the following is equal to $\sqrt{75}$ ?

Answer

√75 can be broken down to √25 * √3. Which simplifies to 5√3.

Compare your answer with the correct one above

Question

Simplify:

$4\sqrt{27}+16\sqrt{75}+3\sqrt{12}$

Answer

4√27 + 16√75 +3√12 =

4(√3)(√9) + 16(√3)(√25) +3(√3)(√4) =

4(√3)(3) + 16(√3)(5) + 3(√3)(2) =

12√3 + 80√3 +6√3= 98√3

Compare your answer with the correct one above

Question

Simplify: $\sqrt{576}$

Answer

In order to take the square root, divide 576 by 2.

$\dpi{100} \sqrt{576}= \sqrt{2}\sqrt{288}=\sqrt{2}\sqrt{2}\sqrt{144}=\sqrt{4}\sqrt{144}=2\cdot 12=24$

Compare your answer with the correct one above

Question

Simplify $(\frac{16}{81})^{1/4}$ .

Answer

$(\frac{16}{81})^{1/4}$

$\frac{16^{1/4}}{81^{1/4}}$

$\frac{(2\cdot 2\cdot 2\cdot 2)^{1/4}}{(3\cdot 3\cdot 3\cdot 3)^{1/4}}$

$\frac{2}{3}$

Compare your answer with the correct one above

Question

What is the simplest way to express $\sqrt{3888}$ ?

Answer

First we will list the factors of 3888:

$3888=3\times1296=3\times\3\times432=3^2\times12\times36=3^2\times12\times12\times3=3^2\times12^2\times3$

$\sqrt{3888}=\sqrt{3^{2}\times 12^{2}\times 3}=\sqrt{3^{2}}\times\sqrt{12^{2}} \times \sqrt{3}=3\times 12\times \sqrt{3}=36\sqrt{3}$

Compare your answer with the correct one above

Question

Simplify $\sqrt{a^{3}b^{4}c^{5}}$ .

Answer

Rewrite what is under the radical in terms of perfect squares:

$x^{2}=x\cdot x$

$x^{4}=x^{2}\cdot x^{2}$

$x^{6}=x^{3}\cdot x^{3}$

Therefore, $\sqrt{a^{3}b^{4}c^{5}}= \sqrt{a^{2}a^{1}b^{4}c^{4}c^{1}}=ab^{2}c^{2}\sqrt{ac}$ .

Compare your answer with the correct one above

Question

Which of the following is equivalent to $\frac{x + \sqrt{3}}{3x + \sqrt{2}}$ ?

Answer

Multiply by the conjugate and the use the formula for the difference of two squares:

$\frac{x + \sqrt{3}}{3x + \sqrt{2}}$

$\frac{x + \sqrt{3}}{3x + \sqrt{2}}\cdot \frac{3x - \sqrt{2}}{3x - \sqrt{2}}$

$\frac{3x^{2} -x \sqrt{2} + 3x\sqrt{3} - \sqrt{6}}{(3x)^{2} - (\sqrt{2})^{2}}$

$\frac{3x^{2} -x \sqrt{2} + 3x\sqrt{3} - \sqrt{6}}{9x^{2} - 2}$

Compare your answer with the correct one above

Question

What is $\sqrt{50}$ ?

Answer

We know that 25 is a factor of 50. The square root of 25 is 5. That leaves $\sqrt{2}$ which can not be simplified further.

Compare your answer with the correct one above

Question

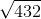
What is $\sqrt{432}$ equal to?

Answer

$\sqrt{432}$

1. We know that , which we can separate under the square root:

$\sqrt{144\cdot 3}$

2. 144 can be taken out since it is a perfect square: $12\cdot12=144$ . This leaves us with:

$12\sqrt{3}$

This cannot be simplified any further.

Compare your answer with the correct one above

Question

Simplfy the following radical $\sqrt{20x^{2}}$ .

Answer

You can rewrite the equation as $\sqrt{20x^2}=(x)\sqrt{5} \cdot \sqrt{4}$ .

This simplifies to $2x\sqrt{5}$ .

Compare your answer with the correct one above

Question

Simplify: $\sqrt{240}$

Answer

Write out the common square factors of the number inside the square root.

$\sqrt{240}= \sqrt{4\times 60}= 2\sqrt{60}$

Continue to find the common factors for 60.

$2\sqrt{60} = 2\sqrt{4\times 15} = 2(2\sqrt{15}) = 4\sqrt{15}$

Since there are no square factors for $\sqrt{15}$ , the answer is in its simplified form. It might not have been easy to see that 16 was a common factor of 240.

The answer is: $4\sqrt{15}$

Compare your answer with the correct one above

Question

Simplify and add:

$\sqrt {64}+\sqrt {27}-\sqrt {81}+\sqrt {3}$ . (Only positive integers)

Answer

Step 1: We need to simplify all the roots:

$\sqrt{64}=\sqrt{16}\cdot\sqrt{4}=4\cdot2=8$

$\sqrt {27}=\sqrt {9}\cdot\sqrt {3}=3\cdot\sqrt{3}=3\sqrt{3}$

$\sqrt {81}=\sqrt{9}\cdot\sqrt{9}=3*3=9$

$\sqrt{3}\rightarrow\sqrt{3}$ (I am not changing this one, it's already simplified)

Step 2: Rewrite the problem with the simplified parts we found in step 1

$8+3\sqrt{3}-9+\sqrt{3}$

Step 3: Combine Like terms:

Numbers:

Roots: $3\sqrt{3}+\sqrt{3}=4\sqrt{3}$

Step 4: Write the final answer. It does not matter how you write it.

$4\sqrt{3}-1$

Compare your answer with the correct one above

Question

Simplify:

$\sqrt{48}$

Answer

To simplify, we want to find some factors of where at least one of the factors is a perfect square.

In this case, and are factors of , and is a perfect square.

We can simplify by saying:

$\sqrt{48} = \sqrt{16\cdot 3} = \sqrt{4^2 \cdot 3} = 4\sqrt{3}$

We could also recognize that two factors of are and . We could approach this way by saying:

$\sqrt{48}=\sqrt{4 \cdot 12} = \sqrt {2^2 \cdot 12} = 2\sqrt{12}$

But we wouldn't stop there. That's because can be further factored:

$2\sqrt{12} = 2\sqrt{4 \cdot 3} = 2\sqrt{2^2 \cdot 3} = 2\cdot 2 \sqrt{3} = 4\sqrt{3}$

Compare your answer with the correct one above

Question

Simplify:

$\sqrt{20,000}$

Answer

To simplify, we want to find factors of where at least one is a perfect square. With this in mind, we find that:

$\sqrt{20,000} = \sqrt{2 \cdot 10,000} = \sqrt{2 \cdot 100^2} = 100\sqrt{2}$

Compare your answer with the correct one above

Tap the card to reveal the answer