Law of Cosines - SAT Math
Card 0 of 20
A triangle has sides that measure 10, 12, and 16. What is the greatest measure of any of its angles (nearest tenth of a degree)?
A triangle has sides that measure 10, 12, and 16. What is the greatest measure of any of its angles (nearest tenth of a degree)?
We are seeking the measure of the angle opposite the side of greatest length, 16.
We can use the Law of Cosines, setting  , and solving for
, and solving for  :
:






We are seeking the measure of the angle opposite the side of greatest length, 16.
We can use the Law of Cosines, setting 

Compare your answer with the correct one above
A triangle has sides that measure 15, 17, and 30. What is the least measure of any of its angles (nearest tenth of a degree)?
A triangle has sides that measure 15, 17, and 30. What is the least measure of any of its angles (nearest tenth of a degree)?
We are seeking the measure of the angle opposite the side of least length, 15.
We can use the Law of Cosines, setting  , and solving for
, and solving for  :
:






We are seeking the measure of the angle opposite the side of least length, 15.
We can use the Law of Cosines, setting 

Compare your answer with the correct one above
Given : with
with  .
.
Which of the following whole numbers is closest to  ?
?
Given :

Which of the following whole numbers is closest to 
Apply the Law of Cosines

setting  and solving for
and solving for  :
:





Of the five choices, 27 comes closest.
Apply the Law of Cosines
setting 

Of the five choices, 27 comes closest.
Compare your answer with the correct one above
Given : with
with  .
.
Evaluate  to the nearest tenth.
to the nearest tenth.
Given :

Evaluate 
Apply the Law of Cosines

setting  and solving for
and solving for  :
:





Apply the Law of Cosines
setting 

Compare your answer with the correct one above
In  :
:



Evaluate the length of  to the nearest tenth of a unit.
to the nearest tenth of a unit.
In 
Evaluate the length of 
The figure referenced is below:
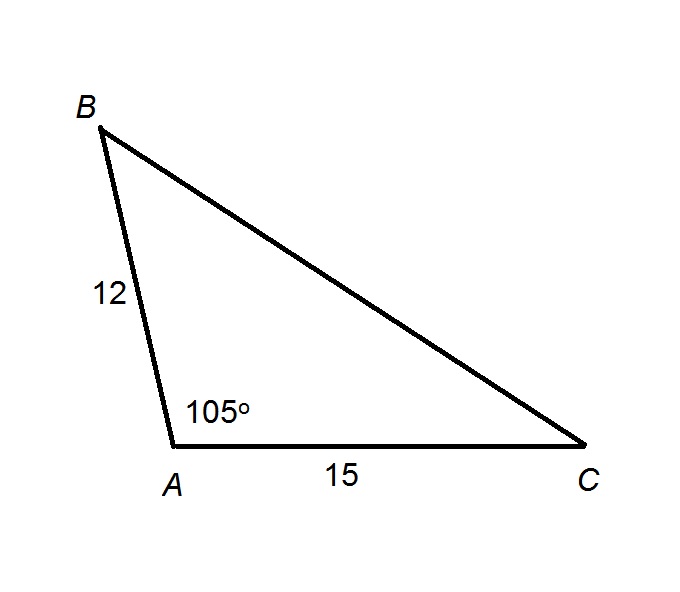
By the Law of Cosines, given the lengths  and
and  of two sides of a triangle, and the measure
of two sides of a triangle, and the measure  of their included angle, the length
of their included angle, the length  of the third side can be calculated using the formula
of the third side can be calculated using the formula

Substituting  ,
,  ,
,  , and
, and  , then evaluating:
, then evaluating:





Taking the square root of both sides:

The figure referenced is below:

By the Law of Cosines, given the lengths 



Substituting 



Taking the square root of both sides:
Compare your answer with the correct one above
A triangle has sides that measure 10, 12, and 16. What is the greatest measure of any of its angles (nearest tenth of a degree)?
A triangle has sides that measure 10, 12, and 16. What is the greatest measure of any of its angles (nearest tenth of a degree)?
We are seeking the measure of the angle opposite the side of greatest length, 16.
We can use the Law of Cosines, setting  , and solving for
, and solving for  :
:






We are seeking the measure of the angle opposite the side of greatest length, 16.
We can use the Law of Cosines, setting 

Compare your answer with the correct one above
A triangle has sides that measure 15, 17, and 30. What is the least measure of any of its angles (nearest tenth of a degree)?
A triangle has sides that measure 15, 17, and 30. What is the least measure of any of its angles (nearest tenth of a degree)?
We are seeking the measure of the angle opposite the side of least length, 15.
We can use the Law of Cosines, setting  , and solving for
, and solving for  :
:






We are seeking the measure of the angle opposite the side of least length, 15.
We can use the Law of Cosines, setting 

Compare your answer with the correct one above
Given : with
with  .
.
Which of the following whole numbers is closest to  ?
?
Given :

Which of the following whole numbers is closest to 
Apply the Law of Cosines

setting  and solving for
and solving for  :
:





Of the five choices, 27 comes closest.
Apply the Law of Cosines
setting 

Of the five choices, 27 comes closest.
Compare your answer with the correct one above
Given : with
with  .
.
Evaluate  to the nearest tenth.
to the nearest tenth.
Given :

Evaluate 
Apply the Law of Cosines

setting  and solving for
and solving for  :
:





Apply the Law of Cosines
setting 

Compare your answer with the correct one above
In  :
:



Evaluate the length of  to the nearest tenth of a unit.
to the nearest tenth of a unit.
In 
Evaluate the length of 
The figure referenced is below:

By the Law of Cosines, given the lengths  and
and  of two sides of a triangle, and the measure
of two sides of a triangle, and the measure  of their included angle, the length
of their included angle, the length  of the third side can be calculated using the formula
of the third side can be calculated using the formula

Substituting  ,
,  ,
,  , and
, and  , then evaluating:
, then evaluating:





Taking the square root of both sides:

The figure referenced is below:

By the Law of Cosines, given the lengths 



Substituting 



Taking the square root of both sides:
Compare your answer with the correct one above
A triangle has sides that measure 10, 12, and 16. What is the greatest measure of any of its angles (nearest tenth of a degree)?
A triangle has sides that measure 10, 12, and 16. What is the greatest measure of any of its angles (nearest tenth of a degree)?
We are seeking the measure of the angle opposite the side of greatest length, 16.
We can use the Law of Cosines, setting  , and solving for
, and solving for  :
:






We are seeking the measure of the angle opposite the side of greatest length, 16.
We can use the Law of Cosines, setting 

Compare your answer with the correct one above
A triangle has sides that measure 15, 17, and 30. What is the least measure of any of its angles (nearest tenth of a degree)?
A triangle has sides that measure 15, 17, and 30. What is the least measure of any of its angles (nearest tenth of a degree)?
We are seeking the measure of the angle opposite the side of least length, 15.
We can use the Law of Cosines, setting  , and solving for
, and solving for  :
:






We are seeking the measure of the angle opposite the side of least length, 15.
We can use the Law of Cosines, setting 

Compare your answer with the correct one above
Given : with
with  .
.
Which of the following whole numbers is closest to  ?
?
Given :

Which of the following whole numbers is closest to 
Apply the Law of Cosines

setting  and solving for
and solving for  :
:





Of the five choices, 27 comes closest.
Apply the Law of Cosines
setting 

Of the five choices, 27 comes closest.
Compare your answer with the correct one above
Given : with
with  .
.
Evaluate  to the nearest tenth.
to the nearest tenth.
Given :

Evaluate 
Apply the Law of Cosines

setting  and solving for
and solving for  :
:





Apply the Law of Cosines
setting 

Compare your answer with the correct one above
In  :
:



Evaluate the length of  to the nearest tenth of a unit.
to the nearest tenth of a unit.
In 
Evaluate the length of 
The figure referenced is below:

By the Law of Cosines, given the lengths  and
and  of two sides of a triangle, and the measure
of two sides of a triangle, and the measure  of their included angle, the length
of their included angle, the length  of the third side can be calculated using the formula
of the third side can be calculated using the formula

Substituting  ,
,  ,
,  , and
, and  , then evaluating:
, then evaluating:





Taking the square root of both sides:

The figure referenced is below:

By the Law of Cosines, given the lengths 



Substituting 



Taking the square root of both sides:
Compare your answer with the correct one above
A triangle has sides that measure 10, 12, and 16. What is the greatest measure of any of its angles (nearest tenth of a degree)?
A triangle has sides that measure 10, 12, and 16. What is the greatest measure of any of its angles (nearest tenth of a degree)?
We are seeking the measure of the angle opposite the side of greatest length, 16.
We can use the Law of Cosines, setting  , and solving for
, and solving for  :
:






We are seeking the measure of the angle opposite the side of greatest length, 16.
We can use the Law of Cosines, setting 

Compare your answer with the correct one above
A triangle has sides that measure 15, 17, and 30. What is the least measure of any of its angles (nearest tenth of a degree)?
A triangle has sides that measure 15, 17, and 30. What is the least measure of any of its angles (nearest tenth of a degree)?
We are seeking the measure of the angle opposite the side of least length, 15.
We can use the Law of Cosines, setting  , and solving for
, and solving for  :
:






We are seeking the measure of the angle opposite the side of least length, 15.
We can use the Law of Cosines, setting 

Compare your answer with the correct one above
Given : with
with  .
.
Which of the following whole numbers is closest to  ?
?
Given :

Which of the following whole numbers is closest to 
Apply the Law of Cosines

setting  and solving for
and solving for  :
:





Of the five choices, 27 comes closest.
Apply the Law of Cosines
setting 

Of the five choices, 27 comes closest.
Compare your answer with the correct one above
Given : with
with  .
.
Evaluate  to the nearest tenth.
to the nearest tenth.
Given :

Evaluate 
Apply the Law of Cosines

setting  and solving for
and solving for  :
:





Apply the Law of Cosines
setting 

Compare your answer with the correct one above
In  :
:



Evaluate the length of  to the nearest tenth of a unit.
to the nearest tenth of a unit.
In 
Evaluate the length of 
The figure referenced is below:

By the Law of Cosines, given the lengths  and
and  of two sides of a triangle, and the measure
of two sides of a triangle, and the measure  of their included angle, the length
of their included angle, the length  of the third side can be calculated using the formula
of the third side can be calculated using the formula

Substituting  ,
,  ,
,  , and
, and  , then evaluating:
, then evaluating:





Taking the square root of both sides:

The figure referenced is below:

By the Law of Cosines, given the lengths 



Substituting 



Taking the square root of both sides:
Compare your answer with the correct one above