Lines, Angles, & Triangles - SAT Math
Card 0 of 30
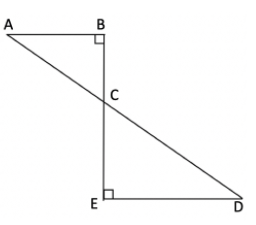
Lines AD and BE intersect at point C as pictured. Which of the following ratios is equal to the ratio of the length of line segment AB to the length of line segment AC?

Lines AD and BE intersect at point C as pictured. Which of the following ratios is equal to the ratio of the length of line segment AB to the length of line segment AC?
Tap to see back →
The two triangles ABC and CED are similar (they share the vertical angle at C and each has a right angle). This means their side lengths are proportional. AB to AC maps to ED to CD in the similar triangle.
The two triangles ABC and CED are similar (they share the vertical angle at C and each has a right angle). This means their side lengths are proportional. AB to AC maps to ED to CD in the similar triangle.
Define these types of triangles by their angle measures: acute, right, and obtuse.
Define these types of triangles by their angle measures: acute, right, and obtuse.
Tap to see back →
Acute (all $<90^{\circ}$), Right ($=90^{\circ}$), Obtuse (one $>90^{\circ}$).
Acute (all $<90^{\circ}$), Right ($=90^{\circ}$), Obtuse (one $>90^{\circ}$).
Definition of a rectangle.
Definition of a rectangle.
Tap to see back →
A parallelogram with four right angles.
A parallelogram with four right angles.
Determine slope of line perpendicular to y = (\t$\frac{1}{2}$)x - 7.
Determine slope of line perpendicular to y = (\t$\frac{1}{2}$)x - 7.
Tap to see back →
-2
-2
Find equation of line through (4, 7) parallel to y = -2x + 3.
Find equation of line through (4, 7) parallel to y = -2x + 3.
Tap to see back →
$Same slope ⇒ y - 7 = -2(x - 4) ⇒ y = -2x + 15.$
$Same slope ⇒ y - 7 = -2(x - 4) ⇒ y = -2x + 15.$
Formula for midpoint between $(x_1, y_1)$ and $(x_2, y_2)$.
Formula for midpoint between $(x_1, y_1)$ and $(x_2, y_2)$.
Tap to see back →
$M = (\tfrac{x_1 + x_2}{2}, \tfrac{y_1 + y_2}{2})$.
$M = (\tfrac{x_1 + x_2}{2}, \tfrac{y_1 + y_2}{2})$.
How can you determine parallel lines in slope-intercept form?
How can you determine parallel lines in slope-intercept form?
Tap to see back →
They have the same slope $(m_1 = m_2).$
They have the same slope $(m_1 = m_2).$
How can you determine perpendicular lines in slope-intercept form?
How can you determine perpendicular lines in slope-intercept form?
Tap to see back →
Their slopes are negative reciprocals: $m_1 m_2 = -1$.
Their slopes are negative reciprocals: $m_1 m_2 = -1$.
How do you find the midpoint between $(x_1, y_1)$ and $(x_2, y_2)$?
How do you find the midpoint between $(x_1, y_1)$ and $(x_2, y_2)$?
Tap to see back →
$((x_1 + x_2)/2, (y_1 + y_2)/2).$
$((x_1 + x_2)/2, (y_1 + y_2)/2).$
How many sides are equal in equilateral, isosceles, and scalene triangles?
How many sides are equal in equilateral, isosceles, and scalene triangles?
Tap to see back →
Equilateral (3 equal sides), Isosceles (2 equal sides), Scalene (no equal sides).
Equilateral (3 equal sides), Isosceles (2 equal sides), Scalene (no equal sides).
If a triangle has sides 7, 24, and 25, is it right?
If a triangle has sides 7, 24, and 25, is it right?
Tap to see back →
Yes, $7^2 + 24^2 = 49 + 576 = 625 = 25^2$.
Yes, $7^2 + 24^2 = 49 + 576 = 625 = 25^2$.
If two lines are perpendicular, what is the measure of each angle formed?
If two lines are perpendicular, what is the measure of each angle formed?
Tap to see back →
$90^{\circ}$.
$90^{\circ}$.
Measure of one interior angle of a regular polygon.
Measure of one interior angle of a regular polygon.
Tap to see back →
$\frac{(n - 2)\times180^{\circ}}{n}$.
$\frac{(n - 2)\times180^{\circ}}{n}$.
Properties of a parallelogram.
Properties of a parallelogram.
Tap to see back →
Opposite sides and angles are equal; diagonals bisect each other.
Opposite sides and angles are equal; diagonals bisect each other.
Relationship between an inscribed angle and its intercepted arc.
Relationship between an inscribed angle and its intercepted arc.
Tap to see back →
An inscribed angle measures half its intercepted arc.
An inscribed angle measures half its intercepted arc.
Angles formed by a transversal cutting parallel lines.
Angles formed by a transversal cutting parallel lines.
Tap to see back →
Corresponding angles are congruent, alternate interior angles are congruent, and same-side interior angles are supplementary.
Corresponding angles are congruent, alternate interior angles are congruent, and same-side interior angles are supplementary.
Sum of angles on a straight line.
Sum of angles on a straight line.
Tap to see back →
$180^{\circ}$.
$180^{\circ}$.
Sum of exterior angles of any polygon.
Sum of exterior angles of any polygon.
Tap to see back →
$360^{\circ}$.
$360^{\circ}$.
Sum of interior angles of an n-sided polygon.
Sum of interior angles of an n-sided polygon.
Tap to see back →
$(n - 2)\times180^{\circ}$.
$(n - 2)\times180^{\circ}$.
What are complementary angles?
What are complementary angles?
Tap to see back →
Two angles whose measures add up to $90^{\circ}$.
Two angles whose measures add up to $90^{\circ}$.
What are supplementary angles?
What are supplementary angles?
Tap to see back →
Two angles whose measures add up to $180^{\circ}$.
Two angles whose measures add up to $180^{\circ}$.
What are vertical angles?
What are vertical angles?
Tap to see back →
Opposite angles formed by two intersecting lines; they are congruent.
Opposite angles formed by two intersecting lines; they are congruent.
What is an altitude of a triangle?
What is an altitude of a triangle?
Tap to see back →
A perpendicular segment from a vertex to the opposite side.
A perpendicular segment from a vertex to the opposite side.
What is an angle of depression?
What is an angle of depression?
Tap to see back →
The angle formed by a horizontal line and the line of sight looking down.
The angle formed by a horizontal line and the line of sight looking down.
What is an angle of elevation?
What is an angle of elevation?
Tap to see back →
The angle formed by a horizontal line and the line of sight looking up.
The angle formed by a horizontal line and the line of sight looking up.
What is the formula for the area of a triangle?
What is the formula for the area of a triangle?
Tap to see back →
$A = \tfrac{1}{2}bh$.
$A = \tfrac{1}{2}bh$.
What is the sum of the interior angles of a triangle?
What is the sum of the interior angles of a triangle?
Tap to see back →
$180^{\circ}$.
$180^{\circ}$.
What side is opposite the largest angle in a triangle?
What side is opposite the largest angle in a triangle?
Tap to see back →
The longest side.
The longest side.
What side is opposite the smallest angle in a triangle?
What side is opposite the smallest angle in a triangle?
Tap to see back →
The shortest side.
The shortest side.
Sum of angles around a point.
Sum of angles around a point.
Tap to see back →
$360^{\circ}$.
$360^{\circ}$.