SAT Math Flashcards - SAT Math
Card 0 of 101
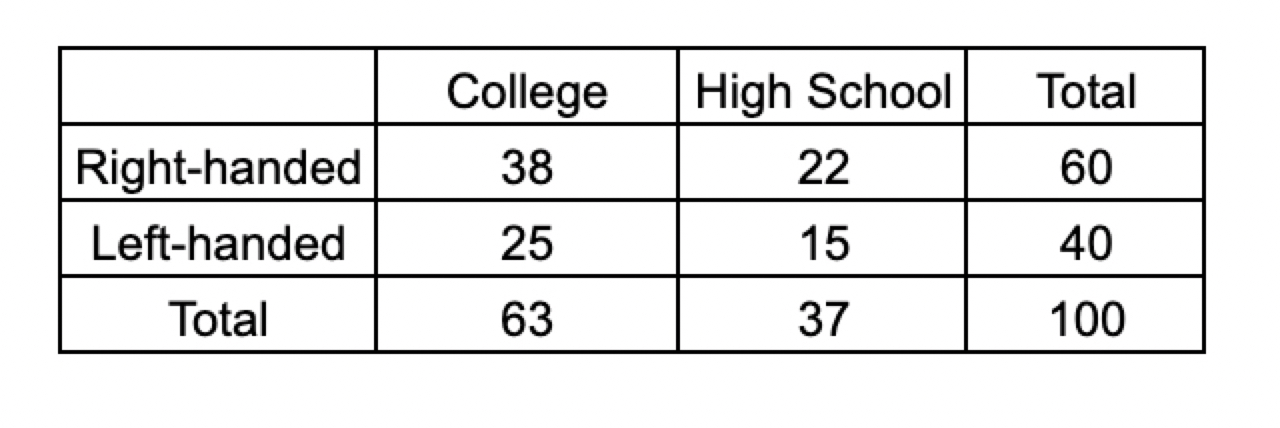
The above table summarizes the 100 baseball players beginning their first professional season, denoting which hand they throw with and whether their most recent experience was with a college team or a high school team. If a left-handed player is chosen at random from this group, what is the probability the he most recently played for a high school team?

The above table summarizes the 100 baseball players beginning their first professional season, denoting which hand they throw with and whether their most recent experience was with a college team or a high school team. If a left-handed player is chosen at random from this group, what is the probability the he most recently played for a high school team?
Tap to see back →
The question asks "if a left-handed player is selected at random" meaning that the denominator should be the total of the left-handed row, which is 40. Then the numerator is the number of left-handed players in the high school column, or 15. The calculation then is 15/40 = 37.5%.
The question asks "if a left-handed player is selected at random" meaning that the denominator should be the total of the left-handed row, which is 40. Then the numerator is the number of left-handed players in the high school column, or 15. The calculation then is 15/40 = 37.5%.
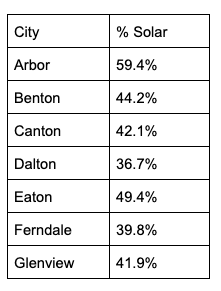
The table above displays, for seven cities in a certain state, the percentage of household electricity that comes from solar power. For the state as a whole, the median percentage is 44.9%. What is the difference between the statewide median percentage and the median percentage for these seven cities?

The table above displays, for seven cities in a certain state, the percentage of household electricity that comes from solar power. For the state as a whole, the median percentage is 44.9%. What is the difference between the statewide median percentage and the median percentage for these seven cities?
Tap to see back →
The median is the middle value in a set of data, so for this set of 7 cities you are looking for the 4th value once the values are arranged in order. The values in order are: 36.7, 39.8, 41.9, 42.1, 44.2, 49.4, 59.4. So the 4th/middle term is 42.1. Since the question asks for the difference between the median and 44.9, you subtract 44.9 - 42.1 to get the answer of 2.8.
The median is the middle value in a set of data, so for this set of 7 cities you are looking for the 4th value once the values are arranged in order. The values in order are: 36.7, 39.8, 41.9, 42.1, 44.2, 49.4, 59.4. So the 4th/middle term is 42.1. Since the question asks for the difference between the median and 44.9, you subtract 44.9 - 42.1 to get the answer of 2.8.
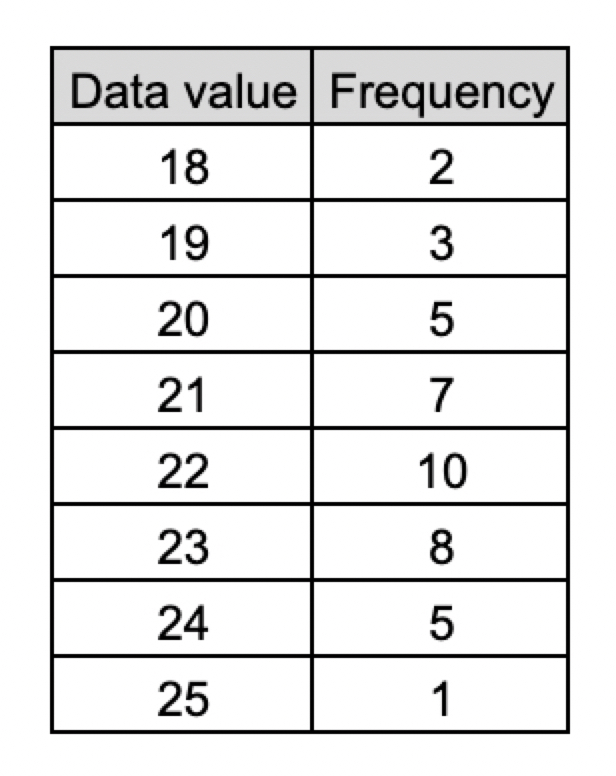
The frequency table summarizes the 41 data values in a data set. What is the maximum data value in the data set?

The frequency table summarizes the 41 data values in a data set. What is the maximum data value in the data set?
Tap to see back →
This question comes down to two key SAT concepts:
-
Understanding a frequency table. Frequency tables tell you how frequently each value occurs in a data table.
-
Read question stems carefully. Here they ask for the maximum data value, meaning you should only look at values in the "data value" column. And 25 - though it only occurs once - is the largest value in the data set and therefore the correct answer.
This question comes down to two key SAT concepts:
-
Understanding a frequency table. Frequency tables tell you how frequently each value occurs in a data table.
-
Read question stems carefully. Here they ask for the maximum data value, meaning you should only look at values in the "data value" column. And 25 - though it only occurs once - is the largest value in the data set and therefore the correct answer.
During a clearance sale, a retailer discounted the original price of its TVs by 25% for the first two weeks of the month, then for the remainder of the month further reduced the price by taking 20% off the sale price. For those who purchased TVs during the last week of the month, what percent of the original price did they have to pay?
During a clearance sale, a retailer discounted the original price of its TVs by 25% for the first two weeks of the month, then for the remainder of the month further reduced the price by taking 20% off the sale price. For those who purchased TVs during the last week of the month, what percent of the original price did they have to pay?
Tap to see back →
With percent problems, the key is often to make sure that you take the percent of the correct value. In this case, the initial 25% off means that customers will pay 75% of the original price. Then for the second discount, keep in mind that the discount is taken off of the sale price, not of the original price. So that's 20% off of the 75% that they did pay, which can be made easier by looking at what the customer does pay: 80% of the 75% sale price. Using fractions, that means they pay:  of the original price, which nets to
of the original price, which nets to  of the original price, or 60%.
of the original price, or 60%.
With percent problems, the key is often to make sure that you take the percent of the correct value. In this case, the initial 25% off means that customers will pay 75% of the original price. Then for the second discount, keep in mind that the discount is taken off of the sale price, not of the original price. So that's 20% off of the 75% that they did pay, which can be made easier by looking at what the customer does pay: 80% of the 75% sale price. Using fractions, that means they pay: 

Data: 3, 5, 7, 9. Find mean.
Data: 3, 5, 7, 9. Find mean.
Tap to see back →
$\frac{3+5+7+9}{4}=6$.
$\frac{3+5+7+9}{4}=6$.
General form of a linear model.
General form of a linear model.
Tap to see back →
$y = mx + b$.
$y = mx + b$.
How are outliers identified in a boxplot?
How are outliers identified in a boxplot?
Tap to see back →
Values more than 1.5 IQRs above $Q_3$ or below $Q_1$.
Values more than 1.5 IQRs above $Q_3$ or below $Q_1$.
How is IQR affected by outliers?
How is IQR affected by outliers?
Tap to see back →
Less affected than range or standard deviation.
Less affected than range or standard deviation.
If $r$ is near -1, what does that mean?
If $r$ is near -1, what does that mean?
Tap to see back →
Strong negative linear relationship.
Strong negative linear relationship.
If $r$ is near 0, what does that mean?
If $r$ is near 0, what does that mean?
Tap to see back →
Little or no linear relationship.
Little or no linear relationship.
If $r$ is near 1, what does that mean?
If $r$ is near 1, what does that mean?
Tap to see back →
Strong positive linear relationship.
Strong positive linear relationship.
If a phone plan costs $20$ per month plus a $30$ activation fee, write a linear cost model.
If a phone plan costs $20$ per month plus a $30$ activation fee, write a linear cost model.
Tap to see back →
$C = 20m + 30$.
$C = 20m + 30$.
If a population of 800 declines 3% per year, write the decay model.
If a population of 800 declines 3% per year, write the decay model.
Tap to see back →
$P = 800(0.97)^t$.
$P = 800(0.97)^t$.
If a substance halves every 10 years, write decay model.
If a substance halves every 10 years, write decay model.
Tap to see back →
$A = A_0(\tfrac{1}{2})^{t/10}$.
$A = A_0(\tfrac{1}{2})^{t/10}$.
If an investment of $1000$ grows by 5% per year, write the model for value after $t$ years.
If an investment of $1000$ grows by 5% per year, write the model for value after $t$ years.
Tap to see back →
$V = 1000(1.05)^t$.
$V = 1000(1.05)^t$.
If data are all identical, what is the standard deviation?
If data are all identical, what is the standard deviation?
Tap to see back →
0
0
If data are skewed left, which is larger: mean or median?
If data are skewed left, which is larger: mean or median?
Tap to see back →
The median is greater than the mean.
The median is greater than the mean.
If data are skewed right, which is larger: mean or median?
If data are skewed right, which is larger: mean or median?
Tap to see back →
The mean is greater than the median.
The mean is greater than the median.
If data are symmetric, how do mean and median compare?
If data are symmetric, how do mean and median compare?
Tap to see back →
They are approximately equal.
They are approximately equal.
If data have a large standard deviation, what does that indicate?
If data have a large standard deviation, what does that indicate?
Tap to see back →
The data are more spread out from the mean.
The data are more spread out from the mean.
If data have a small standard deviation, what does that indicate?
If data have a small standard deviation, what does that indicate?
Tap to see back →
The data are tightly clustered around the mean.
The data are tightly clustered around the mean.
If the population increases by 200 each year from 5,000, write the linear model.
If the population increases by 200 each year from 5,000, write the linear model.
Tap to see back →
$P = 5000 + 200t$.
$P = 5000 + 200t$.
If two data sets have same mean but different spreads, which has higher variability?
If two data sets have same mean but different spreads, which has higher variability?
Tap to see back →
The one with larger SD or IQR.
The one with larger SD or IQR.
If you add 5 to every value in a data set, how does the mean change?
If you add 5 to every value in a data set, how does the mean change?
Tap to see back →
Increases by 5.
Increases by 5.
If you add 5 to every value, how does standard deviation change?
If you add 5 to every value, how does standard deviation change?
Tap to see back →
It stays the same.
It stays the same.
If you multiply every value by 2, how does the mean change?
If you multiply every value by 2, how does the mean change?
Tap to see back →
It doubles.
It doubles.
If you multiply every value by 2, how does the standard deviation change?
If you multiply every value by 2, how does the standard deviation change?
Tap to see back →
It doubles.
It doubles.
What does $f(a) = b$ mean?
What does $f(a) = b$ mean?
Tap to see back →
When $x = a$, the function’s output is $b$.
When $x = a$, the function’s output is $b$.
What does it mean for a function to be one-to-one?
What does it mean for a function to be one-to-one?
Tap to see back →
Each output is produced by exactly one input (passes the horizontal line test).
Each output is produced by exactly one input (passes the horizontal line test).
What does standard deviation measure?
What does standard deviation measure?
Tap to see back →
The average distance of data points from the mean.
The average distance of data points from the mean.
What is interquartile range (IQR)?
What is interquartile range (IQR)?
Tap to see back →
$\text{IQR} = Q_3 - Q_1$.
$\text{IQR} = Q_3 - Q_1$.
What is the definition of standard deviation?
What is the definition of standard deviation?
Tap to see back →
Square root of variance; measures average distance from mean.
Square root of variance; measures average distance from mean.
What is the mean?
What is the mean?
Tap to see back →
The average: $\text{mean} = \frac{\text{sum of all values}}{\text{number of values}}$.
The average: $\text{mean} = \frac{\text{sum of all values}}{\text{number of values}}$.
What is the meaning of the symbol $\ge$?
What is the meaning of the symbol $\ge$?
Tap to see back →
Greater than or equal to.
Greater than or equal to.
What is the meaning of the symbol $\le$?
What is the meaning of the symbol $\le$?
Tap to see back →
Less than or equal to.
Less than or equal to.
What is the meaning of the symbol $<$?
What is the meaning of the symbol $<$?
Tap to see back →
Less than; the value on the left is smaller than the value on the right.
Less than; the value on the left is smaller than the value on the right.
What is the meaning of the symbol $>$?
What is the meaning of the symbol $>$?
Tap to see back →
Greater than; the value on the left is larger than the value on the right.
Greater than; the value on the left is larger than the value on the right.
What is the median?
What is the median?
Tap to see back →
The middle value when data are ordered.
The middle value when data are ordered.
What is the mode?
What is the mode?
Tap to see back →
The most frequently occurring value.
The most frequently occurring value.
What measure of spread is most resistant to outliers?
What measure of spread is most resistant to outliers?
Tap to see back →
Interquartile range (IQR).
Interquartile range (IQR).
What type of change occurs in a linear model?
What type of change occurs in a linear model?
Tap to see back →
Constant difference (additive) change.
Constant difference (additive) change.
When is a regression model appropriate?
When is a regression model appropriate?
Tap to see back →
When data show a roughly linear pattern and residuals are randomly scattered.
When data show a roughly linear pattern and residuals are randomly scattered.
Which measure of center is most affected by outliers?
Which measure of center is most affected by outliers?
Tap to see back →
The mean.
The mean.
Why might averages hide important details?
Why might averages hide important details?
Tap to see back →
They can mask variability or sub-group differences within the data.
They can mask variability or sub-group differences within the data.
A company reports customer satisfaction improved, based on voluntary survey responses. What’s the flaw?
A company reports customer satisfaction improved, based on voluntary survey responses. What’s the flaw?
Tap to see back →
Voluntary response bias; only strongly opinionated customers responded.
Voluntary response bias; only strongly opinionated customers responded.
A company reports that its new tutoring app improved scores in students who used it. There was no control group. What’s the flaw?
A company reports that its new tutoring app improved scores in students who used it. There was no control group. What’s the flaw?
Tap to see back →
No comparison group; improvement could be due to other factors.
No comparison group; improvement could be due to other factors.
A political campaign only surveys its supporters about policy approval. What’s the flaw?
A political campaign only surveys its supporters about policy approval. What’s the flaw?
Tap to see back →
Sample is biased and unrepresentative of the full population.
Sample is biased and unrepresentative of the full population.
A poll finds 60% favor a policy with a margin of error ±5%. What’s the plausible range of support?
A poll finds 60% favor a policy with a margin of error ±5%. What’s the plausible range of support?
Tap to see back →
Between 55% and 65%.
Between 55% and 65%.
A social media post claims 'ice cream sales cause drowning deaths' since both rise in summer. What’s the flaw?
A social media post claims 'ice cream sales cause drowning deaths' since both rise in summer. What’s the flaw?
Tap to see back →
Lurking variable (season): both increase because of warmer weather.
Lurking variable (season): both increase because of warmer weather.
A study claims a tutoring method works better based on only 8 students. What’s the flaw?
A study claims a tutoring method works better based on only 8 students. What’s the flaw?
Tap to see back →
Sample size too small for reliable inference.
Sample size too small for reliable inference.
A survey of 20 mall shoppers found that 90% prefer brand X. The company claims '90% of Americans prefer brand X.' What’s the flaw?
A survey of 20 mall shoppers found that 90% prefer brand X. The company claims '90% of Americans prefer brand X.' What’s the flaw?
Tap to see back →
The sample is too small and not representative of all Americans.
The sample is too small and not representative of all Americans.
An advertisement claims, 'Four out of five dentists recommend our toothpaste.' What’s a possible flaw?
An advertisement claims, 'Four out of five dentists recommend our toothpaste.' What’s a possible flaw?
Tap to see back →
Sample source unclear; could be biased or too small.
Sample source unclear; could be biased or too small.
Define population in a statistical study.
Define population in a statistical study.
Tap to see back →
The entire group of individuals about which information is desired.
The entire group of individuals about which information is desired.
Define sample.
Define sample.
Tap to see back →
A subset of the population used to gather information.
A subset of the population used to gather information.
What is a random sample?
What is a random sample?
Tap to see back →
Every individual in the population has an equal chance of being selected.
Every individual in the population has an equal chance of being selected.
Why can small samples be misleading?
Why can small samples be misleading?
Tap to see back →
They show higher variability and are less likely to represent the population.
They show higher variability and are less likely to represent the population.
A bag has 3 red, 2 blue marbles. On a single draw, what is: $P(\text{red})$?
A bag has 3 red, 2 blue marbles. On a single draw, what is: $P(\text{red})$?
Tap to see back →
$\frac{3}{5}$.
$\frac{3}{5}$.
A box has 4 red and 6 blue marbles. Find $P(\text{blue then red})$ without replacement.
A box has 4 red and 6 blue marbles. Find $P(\text{blue then red})$ without replacement.
Tap to see back →
$\frac{6}{10}\times\frac{4}{9}=\frac{4}{15}$.
$\frac{6}{10}\times\frac{4}{9}=\frac{4}{15}$.
Complement probability of no heads in 3 flips.
Complement probability of no heads in 3 flips.
Tap to see back →
$1-\frac{1}{8}=\frac{7}{8}$.
$1-\frac{1}{8}=\frac{7}{8}$.
Expected value definition.
Expected value definition.
Tap to see back →
Weighted average of all possible outcomes by probability.
Weighted average of all possible outcomes by probability.
Find $P(\text{blue then red})$ with replacement.
Find $P(\text{blue then red})$ with replacement.
Tap to see back →
$\frac{6}{10}\times\frac{4}{10}=\frac{6}{25}$.
$\frac{6}{10}\times\frac{4}{10}=\frac{6}{25}$.
If $P(A)=0.3$ and $P(B|A)=0.5$, find $P(A \text{ and } B)$.
If $P(A)=0.3$ and $P(B|A)=0.5$, find $P(A \text{ and } B)$.
Tap to see back →
$0.15$.
$0.15$.
If $P(A)=0.3$, $P(B)=0.6$, independent events, find $P(A \text{ and } B)$.
If $P(A)=0.3$, $P(B)=0.6$, independent events, find $P(A \text{ and } B)$.
Tap to see back →
$0.18$.
$0.18$.
If $P(A)=0.4$, $P(B)=0.3$, independent, find $P(\text{not A and B})$.
If $P(A)=0.4$, $P(B)=0.3$, independent, find $P(\text{not A and B})$.
Tap to see back →
$(1-0.4)\times0.3=0.18$.
$(1-0.4)\times0.3=0.18$.
If $P(A)=0.4$, $P(B)=0.5$, $P(A \text{ and } B)=0.2$, find $P(A \text{ or } B)$.
If $P(A)=0.4$, $P(B)=0.5$, $P(A \text{ and } B)=0.2$, find $P(A \text{ or } B)$.
Tap to see back →
$0.4+0.5-0.2=0.7$.
$0.4+0.5-0.2=0.7$.
If a coin if flipped twice, what is $P(\text{at least one head})$?
If a coin if flipped twice, what is $P(\text{at least one head})$?
Tap to see back →
$1-(\frac{1}{2})^2=\frac{3}{4}$.
$1-(\frac{1}{2})^2=\frac{3}{4}$.
If two fair dice are rolled, what is $P(\text{both even})$?
If two fair dice are rolled, what is $P(\text{both even})$?
Tap to see back →
$\frac{9}{36}=\frac{1}{4}$.
$\frac{9}{36}=\frac{1}{4}$.
If two fair dice are rolled, what is $P(\text{sum}=7)$?
If two fair dice are rolled, what is $P(\text{sum}=7)$?
Tap to see back →
$\frac{6}{36}=\frac{1}{6}$.
$\frac{6}{36}=\frac{1}{6}$.
In 3 coin flips, $P(\text{exactly 2 heads})$.
In 3 coin flips, $P(\text{exactly 2 heads})$.
Tap to see back →
$\frac{3}{8}$.
$\frac{3}{8}$.
Independent events meaning.
Independent events meaning.
Tap to see back →
Outcome of one does not affect the other.
Outcome of one does not affect the other.
Mutually exclusive events meaning.
Mutually exclusive events meaning.
Tap to see back →
Cannot happen at the same time.
Cannot happen at the same time.
Number of outcomes flipping 3 coins.
Number of outcomes flipping 3 coins.
Tap to see back →
$2^3=8$.
$2^3=8$.
Number of outcomes when rolling two dice.
Number of outcomes when rolling two dice.
Tap to see back →
$6\times6=36$.
$6\times6=36$.
Probability of at least one tail in 2 flips.
Probability of at least one tail in 2 flips.
Tap to see back →
$1-\frac{1}{4}=\frac{3}{4}$.
$1-\frac{1}{4}=\frac{3}{4}$.
Probability of drawing a red card from a deck.
Probability of drawing a red card from a deck.
Tap to see back →
$\frac{26}{52}=\frac{1}{2}$.
$\frac{26}{52}=\frac{1}{2}$.
Probability of drawing an ace from a deck.
Probability of drawing an ace from a deck.
Tap to see back →
$\frac{4}{52}=\frac{1}{13}$.
$\frac{4}{52}=\frac{1}{13}$.
Probability of exactly one head in 2 flips.
Probability of exactly one head in 2 flips.
Tap to see back →
$\frac{2}{4}=\frac{1}{2}$.
$\frac{2}{4}=\frac{1}{2}$.
Probability of flipping heads on one coin.
Probability of flipping heads on one coin.
Tap to see back →
$\frac{1}{2}$.
$\frac{1}{2}$.
Probability of neither A nor B.
Probability of neither A nor B.
Tap to see back →
$1-P(A \text{ or } B)$.
$1-P(A \text{ or } B)$.
Probability of no heads in three coin flips.
Probability of no heads in three coin flips.
Tap to see back →
$(\frac{1}{2})^3=\frac{1}{8}$.
$(\frac{1}{2})^3=\frac{1}{8}$.
Probability of rolling a 6 then a 6.
Probability of rolling a 6 then a 6.
Tap to see back →
$(\frac{1}{6})^2=\frac{1}{36}$.
$(\frac{1}{6})^2=\frac{1}{36}$.
Probability of rolling a number greater than 4 on one die.
Probability of rolling a number greater than 4 on one die.
Tap to see back →
$\frac{2}{6}=\frac{1}{3}$.
$\frac{2}{6}=\frac{1}{3}$.
Probability of rolling an odd number on one die.
Probability of rolling an odd number on one die.
Tap to see back →
$\frac{3}{6}=\frac{1}{2}$.
$\frac{3}{6}=\frac{1}{2}$.
Probability of rolling even then odd.
Probability of rolling even then odd.
Tap to see back →
$\frac{1}{2}\times\frac{1}{2}=\frac{1}{4}$.
$\frac{1}{2}\times\frac{1}{2}=\frac{1}{4}$.
Probability of selecting a letter from 'SAT' that is a vowel.
Probability of selecting a letter from 'SAT' that is a vowel.
Tap to see back →
$\frac{1}{3}$.
$\frac{1}{3}$.
A student claims, 'My school’s average SAT score is 1400, so every student scores around 1400.' What’s the flaw?
A student claims, 'My school’s average SAT score is 1400, so every student scores around 1400.' What’s the flaw?
Tap to see back →
Confuses mean with distribution; average doesn’t imply all are near that value.
Confuses mean with distribution; average doesn’t imply all are near that value.
Probability of two independent events both happening.
Probability of two independent events both happening.
Tap to see back →
Multiply their probabilities.
Multiply their probabilities.
Sum of probabilities of all possible outcomes.
Sum of probabilities of all possible outcomes.
Tap to see back →
1
1
What is the addition rule for mutually exclusive events?
What is the addition rule for mutually exclusive events?
Tap to see back →
$P(A \text{ or } B) = P(A) + P(B)$.
$P(A \text{ or } B) = P(A) + P(B)$.
What is the conditional probability formula?
What is the conditional probability formula?
Tap to see back →
$P(A|B)=\frac{P(A \text{ and } B)}{P(B)}$.
$P(A|B)=\frac{P(A \text{ and } B)}{P(B)}$.
What is the formula for complementary probability?
What is the formula for complementary probability?
Tap to see back →
$P(\text{not A}) = 1 - P(A)$.
$P(\text{not A}) = 1 - P(A)$.
What is the formula for probability of 'at least one' event?
What is the formula for probability of 'at least one' event?
Tap to see back →
$1 - P(\text{none})$.
$1 - P(\text{none})$.
What is the fundamental counting principle?
What is the fundamental counting principle?
Tap to see back →
Multiply the number of outcomes for each stage.
Example: if a restaurant offers a choice of 3 sandwiches, 2 sides, and 4 drinks in its value meals, multiply 3 x 2 x 4 to see 24 total value meal combinations.
Multiply the number of outcomes for each stage.
Example: if a restaurant offers a choice of 3 sandwiches, 2 sides, and 4 drinks in its value meals, multiply 3 x 2 x 4 to see 24 total value meal combinations.
What is the general addition rule in probability?
What is the general addition rule in probability?
Tap to see back →
$P(A \text{ or } B) = P(A) + P(B) - P(A \text{ and } B)$.
$P(A \text{ or } B) = P(A) + P(B) - P(A \text{ and } B)$.
What is the general formula for probability of a favorable outcome?
What is the general formula for probability of a favorable outcome?
Tap to see back →
$P(A)=\frac{\text{favorable outcomes}}{\text{total outcomes}}$.
$P(A)=\frac{\text{favorable outcomes}}{\text{total outcomes}}$.
What is the multiplication rule for independent events?
What is the multiplication rule for independent events?
Tap to see back →
$P(A \text{ and } B) = P(A)P(B)$.
$P(A \text{ and } B) = P(A)P(B)$.
What is the range of probability values.
What is the range of probability values.
Tap to see back →
Between 0 and 1 inclusive.
Between 0 and 1 inclusive.
Probability of selecting a vowel from English alphabet.
Probability of selecting a vowel from English alphabet.
Tap to see back →
$\frac{5}{26}$.
$\frac{5}{26}$.
Data: 1, 2, 2, 4. Find mode.
Data: 1, 2, 2, 4. Find mode.
Tap to see back →
2
2
Data: 1, 3, 5, 7, 9. Find mean and median.
Data: 1, 3, 5, 7, 9. Find mean and median.
Tap to see back →
Both are 5 (symmetric distribution).
Both are 5 (symmetric distribution).
Data: 2, 4, 8. Find median.
Data: 2, 4, 8. Find median.
Tap to see back →
4
4