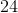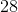SAT Math - Faces, Face Area, and Vertices

A convex polyhedron with eighteen faces and forty edges has how many vertices?

Explanation

The number of vertices, edges, and faces of a convex polygon——are related by the Euler's formula:

Therefore, set and solve for :

The polyhedron has twenty-four faces.

A regular icosahedron has twenty congruent faces, each of which is an equilateral triangle.

A given regular icosahedron has edges of length four inches. Give the total surface area of the icosahedron.

$80 \sqrt{3} \textrm{ in}^{2}$

$80 \sqrt{2} \textrm{ in}^{2}$

$40 \sqrt{3} \textrm{ in}^{2}$

$40 \sqrt{2} \textrm{ in}^{2}$

$80 \textrm{ in}^{2}$

Explanation

The area of an equilateral triangle is given by the formula

$A = \frac{s^{2}\sqrt{3}}{4}$

Since there are twenty equilateral triangles that comprise the surface of the icosahedron, the total surface area is

$SA = 20 A = 20 \cdot \frac{s^{2}\sqrt{3}}{4} = 5 s^{2}\sqrt{3}$

Substitute :

$SA = 5 \cdot 4^{2}\sqrt{3} = 5 \cdot 16 \sqrt{3} = 80 \sqrt{3}$ square inches.

How many edges does a polyhedron with eight vertices and twelve faces have?

Insufficient information is given to answer the question.

Explanation

By Euler's Formula, the relationship between the number of vertices , the number of faces , and the number of edges of a polyhedron is

Set and and solve for :

The polyhedron has eighteen edges.

A regular tetrahedron has four congruent faces, each of which is an equilateral triangle.

The total surface area of a given regular tetrahedron is 600 square centimeters. To the nearest tenth of a centimeter, what is the length of each edge?

$18.6 \textrm{ cm}$

$37.2\textrm{ cm}$

$24.5 \textrm{ cm}$

$12.2 \textrm{ cm}$

$11.9 \textrm{ cm}$

Explanation

The total surface area of the tetrahedron is 600 square centimeters; since the tetrahedron comprises four congruent faces, each has area $600 \div 4 = 150$ square centimeters.

The area of an equilateral triangle is given by the formula

$A = \frac{s^{2}\sqrt{3}}{4}$

Set and solve for :

$\frac{s^{2}\sqrt{3}}{4} = 150$

$\frac{s^{2}\sqrt{3}}{4} \cdot \frac{4}{\sqrt{3}}=1 50 \cdot \frac{4}{\sqrt{3}}$

$s^{2} = \frac{600}{ \sqrt{3}} \approx \frac{600}{1.732} \approx 346.41$

$s \approx \sqrt{346.41} \approx 18.6$ centimeters.

How many faces does a polyhedron with nine vertices and sixteen edges have?

Explanation

By Euler's Formula, the relationship between the number of vertices , the number of faces , and the number of edges of a polyhedron is

Set and and solve for :

The polyhedron has nine faces.

How many edges does a polyhedron with fourteen vertices and five faces have?

Explanation

By Euler's Formula, the relationship between the number of vertices , the number of faces , and the number of edges of a polyhedron is

Set and and solve for :

The polyhedron has seventeen edges.

How many faces does a polyhedron with ten vertices and sixteen edges have?

Explanation

By Euler's Formula, the relationship between the number of vertices , the number of faces , and the number of edges of a polyhedron is

Set and and solve for :

The polyhedron has eight faces.

A regular octahedron has eight congruent faces, each of which is an equilateral triangle.

The total surface area of a given regular octahedron is 400 square centimeters. To the nearest tenth of a centimeter, what is the length of each edge?

$10.7 \textrm{ cm}$

$21.5 \textrm{ cm}$

$11.9 \textrm{ cm}$

$23.8 \textrm{ cm}$

$14.1 \textrm{ cm}$

Explanation

The total surface area of the octahedron is 400 square centimeters; since the octahedron comprises eight congruent faces, each has area $400 \div 8 = 50$ square centimeters.