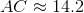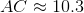Finding Sides
Help Questions
SAT Math › Finding Sides
Which of the following describes a triangle with sides one kilometer, 100 meters, and 100 meters?
The triangle cannot exist.
The triangle is acute and equilateral.
The triangle is obtuse and isosceles, but not equilateral.
The triangle is acute and isosceles, but not equilateral.
The triangle is obtuse and scalene.
Explanation
One kilometer is equal to 1,000 meters, so the triangle has sides of length 100, 100, and 1,000. However,
That is, the sum of the least two sidelengths is not greater than the third. This violates the Triangle Inequality, and this triangle cannot exist.

The above figure is a regular pentagon. Evaluate 
Explanation
Two sides of the triangle formed measure 4 each; the included angle is one angle of the regular pentagon, which measures
The length of the third side can be found by applying the Law of Cosines:
where 

Note: figure NOT drawn to scale.
Refer to the above diagram.

Which of the following expressions is equal to 
Explanation
By the Law of Sines,

Substitute 


We can solve for 

Note: figure NOT drawn to scale.
Refer to the triangle in the above diagram.
Evaluate 
Explanation
By the Law of Cosines,
Substitute 

Note: figure NOT drawn to scale.
Refer to the triangle in the above diagram.
Evaluate 
Explanation
By the Law of Cosines,
Substitute 
Regular Pentagon 
To the nearest tenth, give the length of diagonal 
Explanation
The perimeter of the regular pentagon is 60, so each side measures one fifth of this, or 12. Also, each interior angle of a regular pentagon measures 
The pentagon, along with diagonal 

A triangle 


where 



Setting 


Taking the square root of both sides:

the correct choice.

The above figure is a regular decagon. Evaluate 
Explanation
Two sides of the triangle formed measure 6 each; the included angle is one angle of the regular decagon, which measures
![m = \left [\frac{180(10-2)}{10} \right ] ^{\circ }= 144^{\circ }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/219688/gif.latex)
Since we know two sides and the included angle of the triangle in the diagram, we can apply the Law of Cosines,
with 







Explanation
A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.

Thus, we can consider the right triangle 



Using the Pythagorean Theorem,





5
12
15
24
30
Explanation
A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.

Thus, we can consider the right triangle 



Because the diagonals bisect each other, we know:
Using the Pythagorean theorem,
Regular Pentagon 




Explanation
The perimeter of the regular pentagon is 35, so each side measures one fifth of this, or 7. Also, since 


Also, each interior angle of a regular pentagon measures 
Below is the pentagon in question, with 


A triangle 



where 



Setting 



Taking the square root of both sides:

the correct choice.






![m = \left [\frac{180(5-2)}{5} \right ] ^{\circ }= 108^{\circ }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/216649/gif.latex)