Range and Domain
Help Questions
SAT Math › Range and Domain
Which of the following is NOT a function?
Explanation
A function has to pass the vertical line test, which means that a vertical line can only cross the function one time. To put it another way, for any given value of 












What is the domain of the following function? Please use interval notation.
Explanation
A basic knowledge of absolute value and its functions is valuable for this problem. However, if you do not know what the typical shape of an absoluate value function looks like, one can always plug in 
Upon doing so, we learn that the 
If we plug in -100000 for 

If we plug in 100000 for 

Additionally, if we plug in any value for 

**Extra Note: Due to the absolute value notation, the negative (-) next to the 


Give the domain of the function below.
Explanation
The domain is the set of possible value for the 

Now we can solve for 
There is no real value of 
The radicand is always positive, and 


What is the range of the equation 
Explanation
The equation given represents a horizontal line. This means that every y-value on the domain is equal to 
The answer is:
What is the range of the function 
All real numbers except 
All real numbers.
All real numbers except 
All real numbers except 
Explanation
Start by considering the term 






If 

Explanation
Using 



Therefore 

What is the domain of the function
Explanation
The domain of a function is all the x-values that in that function. The function 
What is the domain of the function?
Explanation
Notice this function resembles the parent function 

Set up an inequality to determine the domain of 
Subtract three from both sides.
Divide by negative ten on both sides. The sign will switch.
The domain is:
Domain: All real numbers
Range:
Domain: All real numbers
Range:
Explanation
The domain includes the values that go into a function (the x-values) and the range are the values that come out (the 


Find the domain:
Explanation
To find the domain, find all areas of the number line where the fraction is defined.

Factor by finding two numbers that sum to -2 and multiply to 1. These numbers are -1 and -1.


















![[\frac{1}{5}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010651/gif.latex)

![[\frac{1}{5},\infty]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010655/gif.latex)

![[-\frac{1}{5}, \frac{1}{5}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010658/gif.latex)
![[\frac{1}{5}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010732/gif.latex)



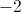






![[-\infty ,\infty]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/878321/gif.latex)













 is a sine curve. What are the domain and range of this function?
is a sine curve. What are the domain and range of this function?









