Solving Inequalities
Help Questions
SAT Math › Solving Inequalities
What is the solution set for 
Explanation
Start by finding the roots of the equation by changing the inequality to an equal sign.
Now, make a number line with the two roots:

Pick a number less than 
For 


Next, pick a number between 
For 


Finally, pick a number greater than 
For 


Thus, the solution set for this inequality is 
Solve the inequality:
Explanation
Add 26 on both sides.
Divide by two on both sides.
The answer is:
Solve the inequality:
Explanation
Subtract nine from both sides.
Divide by negative 3 on both sides. We will need to switch the sign.
The answer is:
Give the solution set of the inequality
Explanation
Two numbers of like sign have a positive quotient.
Therefore, 


To find this set of points, we identify the zeroes of both expressions.
Since 



Choose 

Choose 

Choose 

The solution set is
Solve for x.
Explanation
Solving inequalities is very similar to solving an equation. We must start by isolating x by moving the terms farthest from it to the other side of the inequality. In this case, subtract 2from each side.
Now, divide both sides by 2.
Solve: 
Explanation
First, we distribute the 
Now we solve for x, taking care to change the direction of the inequality if we divide by a negative number:
Solve the inequality:
Explanation
Add six on both sides.
Divide by three on both sides.
The answer is:
Give the solution set of the inequality:
Explanation
First, find the zeroes of the numerator and the denominator. This will give the boundary points of the intervals to be tested.

Since the numerator may be equal to 0, 


Now, test each of four intervals for inclusion in the solution set by substituting one test value from each:
Let's test 
This is false, so 
Let's test 
This is true, so 
Let's test 
This is false, so 
Let's test 
This is true, so 
The solution set is therefore ![\left [-9, 2 \right ] \cup (6, \infty)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/243171/gif.latex)
Solve:
Explanation
The first thing we can do is clean up the right side of the equation by distributing the 
Now we can combine further. At some point, we'll have to divide by a negative number, which will change the direction of the inequality.
Solve the inequality:
Explanation
Add seven on both sides.
Divide by three on both sides.
The answer is:


















































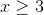
























![\left [-9, 2 \right ] \cup (6, \infty)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/243122/gif.latex)

![(- \infty, -9] \cup [2, 6)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/243124/gif.latex)
![(- \infty, -2] \cup (6, 9]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/243125/gif.latex)
![(- \infty, -9] \cup (6, \infty)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/243126/gif.latex)















































