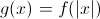SAT Math - Transformations

Axes_1

Refer to the above figure.

Which of the following functions is graphed?

$g(x) =\left | \frac{1}{3} x-\frac{4}{3} \right |$

$g(x) =\left | \frac{1}{3} x+\frac{4}{3} \right |$

Explanation

Below is the graph of :

Axes_1

If the graph of is translated by shifting each point to the point , the graph of

is formed. If the graph is then shifted right by four units, the new graph is

Since the starting graph was , the final graph is

, or

Axes_1

Refer to the above figure.

Which of the following functions is graphed?

$g(x) =\left | \frac{1}{4}x \right |- 4$

$g(x) =\left | \frac{1}{4}x-1 \right |$

$g(x) =\left | \frac{1}{4}x+1 \right |$

Explanation

Below is the graph of :

Axes_1

If the graph of is translated by shifting each point to the point $\left ( x, \frac{1}{4}y \right )$ , the graph of

$g(x) = \frac{1}{4}f(x)$

is formed. If the graph is then shifted down by four units, the new graph is

$g(x) = \frac{1}{4}f(x)- 4$ .

Since the starting graph was , the final graph is

$g(x) = \frac{1}{4}|x|- 4$ , or

$g(x) =\left | \frac{1}{4}x \right |- 4$

Axes_1

Refer to the above figure.

Which of the following functions is graphed?

$g(x) =\left | \frac{1}{3} x- \frac{2}{3} \right |$

$g(x) =\left | \frac{1}{3} x+ \frac{2}{3} \right |$

$g(x) =\left | \frac{1}{3} x \right |+2$

Explanation

Below is the graph of :

Axes_1

If the graph of is translated by shifting each point to the point $\left ( x, \frac{1}{3}y \right )$ , the graph of

$g(x) = \frac{1}{3}f(x)$

is formed. If the graph is then shifted right by two units, the new graph is

$g(x) = \frac{1}{3}f(x-2)$

Since the starting graph was , the final graph is

$g(x) = \frac{1}{3} |x-2|$ , or

$g(x) =\left | \frac{1}{3} x- \frac{2}{3} \right |$

A regular pentagon is graphed in the standard (x,y) coordinate plane. Which of the following are the coordinates for the vertex P?

Screen_shot_2013-06-03_at_1.02.45_pm

Explanation

Regular pentagons have lines of symmetry through each vertex and the center of the opposite side, meaning the y-axis forms a line of symmetry in this instance. Therefore, point P is negative b units in the x-direction, and c units in the y-direction. It is a reflection of point (b,c) across the y-axis.

Axes_1

Refer to the above figure.

Which of the following functions is graphed?

$g(x) =\left | \frac{1}{2} x \right |+ 3$

$g(x) = \left |3x + \frac{3}{2} \right |\textup{}$

Explanation

Below is the graph of :

Axes_1

If the graph of is translated by shifting each point to the point , the graph of

is formed. If the graph is then shifted upward by three units, the new graph is

Since the starting graph was , the final graph is

, or,

Line m passes through the points (–4, 3) and (2, –6). If line q is generated by reflecting m across the line y = x, then which of the following represents the equation of q?

3x + 2y = 6

3x + 2y = 18

2x + 3y = –6

2x + 3y = 6

–2x + 3y = 6

Explanation

When a point is reflected across the line y = x, the x and y coordinates are switched. In other words, the point (a, b) reflected across the line y = x would be (b, a).

Thus, if line m is reflected across the line y = x, the points that it passes through will be reflected across the line y = x. As a result, since m passes through (–4, 3) and (2, –6), when m is reflected across y = x, the points it will pass through become (3, –4) and (–6, 2).

Because line q is a reflection of line m across y = x, q must pass through the points (3, –4) and (–6, 2). We know two points on q, so if we determine the slope of q, we can then use the point-slope formula to find the equation of q.

First, let's find the slope between (3, –4) and (–6, 2) using the formula for slope between the points (x1, y1) and (x2, y2).

slope = (2 – (–4))/(–6 –3)

= 6/–9 = –2/3

Next, we can use the point-slope formula to find the equation for q.

y – y1 = slope(x – x1)

y – 2 = (–2/3)(x – (–6))

Multiply both sides by 3.

3(y – 2) = –2(x + 6)

3y – 6 = –2x – 12

Add 2x to both sides.

2x + 3y – 6 = –12

Add six to both sides.

2x + 3y = –6

The answer is 2x + 3y = –6.

Let f(x) = x3 – 2x2 + x +4. If g(x) is obtained by reflecting f(x) across the y-axis, then which of the following is equal to g(x)?

–x3 – 2x2 – x – 4

–x3 + 2x2 – x + 4

x3 + 2x2 + x + 4

–x3 – 2x2 – x + 4

x3 – 2x2 – x + 4

Explanation

In order to reflect a function across the y-axis, all of the x-coordinates of every point on that function must be multiplied by negative one. However, the y-values of each point on the function will not change. Thus, we can represent the reflection of f(x) across the y-axis as f(-x). The figure below shows a generic function (not f(x) given in the problem) that has been reflected across the y-axis, in order to offer a better visual understanding.

Therefore, g(x) = f(–x).

f(x) = x3 – 2x2 + x – 4

g(x) = f(–x) = (–x)3 – 2(–x)2 + (–x) + 4

g(x) = (–1)3x3 –2(–1)2x2 – x + 4

g(x) = –x3 –2x2 –x + 4.

The answer is –x3 –2x2 –x + 4.

Let $\small f(x)=x^5-2x^4-6x^3+x^2+5x$ . If we let $\small g(x)$ equal $\small f(x)$ when it is flipped across the y-axis, what is the equation for $\small \small g(x)$ ?

$\small -x^5-2x^4+6x^3+x^2-5x$

$\small x^5+2x^4-6x^3-x^2+5x$

$\small -x^5+2x^4+6x^3-x^2-5x$

$\small x^5+2x^4+6x^3+x^2+5x$

$\small x^5-2x^4+6x^3-x^2+5x$

Explanation

When a function $\small f(x)$ is flipped across the y-axis, the resulting function $\small g(x)$ is equal to $\small f(-x)$ . Therefore, to find our $\small g(x)$ , we must substitute in $\small -x$ for every $\small x$ is our equation: