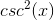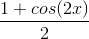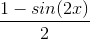SAT Math - Trigonometric Identities

Using trigonometric identities prove whether the following is valid:

$\sin^{2}A + \cot^{2}A = \frac{2\sin^{4}A +2\cos^{2}A}{1 - \cos 2A}$

True

False

Uncertain

Only in the range of: $0 < A < \frac{\pi}{2}$

Only in the range of: $0 < A < 2\pi$

Explanation

We can work with either side of the equation as we choose. We work with the right hand side of the equation since there is an obvious double angle here. We can factor the numerator to receive the following:

$\sin^{2}A + \cot^{2}A = \frac{2\left(\sin^{4}A + \cos^{2}A\right)}{1-\cos 2A}$

Next we note the power reducing formula for sine so we can extract the necessary components as follows:

$\sin^{2}A + \cot^{2}A = \frac{2}{1-\cos 2A}\left(\sin^{4}A + \cos^{2}A\right)$

The power reducing formula must be inverted giving:

$\sin^{2}A + \cot^{2}A = \frac{1}{\sin^{2}A}\left(\sin^{4}A + \cos^{2}A\right)$

Now we can distribute and reduce:

$\sin^{2}A + \cot^{2}A = \sin^{2}A + \frac{\cos^{2}A}{\sin^{2}A}$

Finally recalling the basic identity for the cotangent:

$\sin^{2}A + \cot^{2}A = \sin^{2}A + \cot^{2}A$

This proves the equivalence.

If $\sin \beta = \frac{3}{5}$ and $0 < \beta < \frac{\pi}{2}$ , evaluate $\cos 2\beta$ .

$\frac{7}{25}$

$\frac{9}{25}$

$\frac{16}{25}$

$\frac{4}{5}$

$\frac{8}{5}$

Explanation

The easiest identity to use here is:

$\cos 2\beta = 1 - 2 \sin^2 \beta$

Substituting in the given values we get:

$= 1 - 2 \left ( \frac{3}{5} \right )^2 = 1 - \frac{18}{25} = \frac{7}{25}$

According to the trigonometric identities,

$\frac{sin(x)}{cos(x)}$

$\frac{1}{tan(x)}$

Explanation

The trigonometric identity , is an important identity to memorize.

Some other identities that are important to know are:

$\frac{sin(x)}{cos(x)}=tan(x)$

$cot(x)=\frac{1}{tan(x)}$

Simplify using the trigonometric power reducing formula.

$\frac{1-cos(2x)}{2}$

$\frac{1+cos(2x)}{2}$

$\frac{1-sin(2x)}{2}$

$\frac{1+sin(2x)}{2}$

$\frac{1-cos(2x)}{1+cos(2x)}$

Explanation

The power-reducing formulas state that:

$sin^2(x)=\frac{1-cos(2x)}{2}$

$cos^2(x)=\frac{1+cos(2x)}{2}$

$tan^2(x)=\frac{1-cos(2x)}{1+cos(2x)}$

Simplify the expression $\frac{\sin x}{1 + \cos x} + \frac{1 + \cos x}{\sin x}$ .

$2\csc x$

$2\sec x$

$2\sin x + 2\cos x$

$1 + \tan x$

$\cot x - 1$

Explanation

$\frac{\sin x}{1 + \cos x} + \frac{1 + \cos x}{\sin x}$

Find a common denominator

$\frac{(\sin x) \sin x}{(1 + \cos x) \sin x} + \frac{(1 + \cos x)(1 + \cos x)}{\sin x (1 + \cos x)}$

Multiply the numerators and leave the denominators factored

$\frac{ \sin^2 x}{(1 + \cos x) \sin x} + \frac{1 + 2\cos x + \cos^2 x}{\sin x (1 + \cos x)}$

Add numerators

$\frac{1 + 2\cos x + \cos^2 x + \sin^2 x}{\sin x (1 + \cos x)}$

Pythagorean identity

$\frac{1 + 2\cos x + 1}{\sin x (1 + \cos x)}$

Combine like terms

$\frac{2 + 2\cos x}{\sin x (1 + \cos x)}$

Factor numerator

$\frac{2(1 + \cos x)}{\sin x (1 + \cos x)}$

Reduce

$\frac{2}{\sin x}$

Reciprocal identity

$2\csc x$

Which of the following is the simplified version of $\cot x \sec x \cos x \sin x$ ?

$\cos x$

$\csc x$

$\tan x$

$\cot x$

$\sec x$

Explanation

To solve this problem we need to rewrite it in terms of $\cos x$ and $\sin x$ .

Rewriting cotangent we get the following.

$\cot x= \frac{1}{\tan x}\rightarrow \tan x=\frac{\sin x}{\cos x} \rightarrow \cot x=\frac{\cos x}{\sin x}$

Rewriting secant we get the following.

$\sec x=\frac{1}{\cos x}$

Thus, we can substitute these identities into our original problem and simplify.

$\cot x \sec x \cos x \sin x = \frac{\cos x}{\sin x} \cdot \frac{1}{\cos x} \cdot \frac{\cos x}{1} \cdot \frac{\sin x}{1} = \cos x$

Use the power reducing formulas for trigonometric functions to reduce and simplify the following equation:

$\sin^{2}A \cos^{2} A$

$\frac{3 + \cos 4A}{8}$

$\frac{1 + 2\cos A}{2}$

$\frac{1 + \cos^{2}2A}{2}$

$1 + \cos^{2}A$

$1 + \cos 2A$

Explanation

The power reducing formulas for both sine and cosine differ in only the operation in the numerator. Applying the power reducing formulas here we get:

$\frac{1-\cos 2A}{2}\times \frac{1 + \cos 2A}{2}$

Multiplying the binomials in the numerator and multiplying the denominators:
$\frac{1-\cos 2A + \cos 2A - \cos^{2} 2A}{4}$

Reducing the numerator:

$\frac{1+\cos^{2}2A}{4}$

We again use the power reducing formula for cosine as follows:

$\frac{1 + \frac{1 + \cos 4A}{2}}{4}$

Combining the numerator by determining a common denominator:

$\frac{\frac{3 + \cos 4A}{2}}{4}$

Now simply reducing the double fraction:

$\frac{3 + \cos 4A}{8}$

Using trigonometric identities, determine whether the following is valid:

$\sin^{2} A \cos^{2} A = \frac{1-\cos^{4}A-2\cos^{2}A\sin^{2}A + \sin^{4}A}{4}$

False

True

Uncertain

Only valid in the range of: $0 < A < 2\pi$

Only valid in the range of: $0 < A < \frac{\pi}{2}$

Explanation

In this case we choose to work with the side that appears to be simpler, the left hand side. We begin by using the power reducing formulas:

$\frac{1-\cos 2A}{2}\frac{1+\cos 2A}{2} = \frac{1-\cos^{4}A -2\cos^{2}A\sin^{2}A+\sin^{4}A}{4}$

Next we perform the multiplication on the numerator:

$\frac{1-\cos^{2}2A}{4} = \frac{1-\cos^{4}A -2\cos^{2}A\sin^{2}A+\sin^{4}A}{4}$

The next step we take is to remove the double angle, since there is no double angle in the alleged solution:

$\frac{1 - \left(\cos^{2}A -\sin^{2}A\right )^{2}}{4}=\frac{1-\cos^{4}A -2\cos^{2}A\sin^{2}A+\sin^{4}A}{4}$

Finally we multiply the binomials in the numerator on the left hand side to determine if the equivalence holds:

$\frac{1-\cos^{4}A +2\cos^{2}A\sin^{2}A-\sin^{4}A}{4} = \frac{1-\cos^{4}A -2\cos^{2}A\sin^{2}A+\sin^{4}A}{4}$

We see that the equivalence does not hold.

Simplify the expression:

$\csc\theta(\sin\theta+\cos\theta \cot\theta)$

$\csc^{2}\theta$

$\cos\theta$

$\frac{1}{\csc^{2}\theta }$

$-\sec^{2}\theta$

Explanation

The first step in solving this equation is to distribute :

$\csc\theta(\sin\theta +\cos\theta \cot\theta ) = \csc \theta\sin\theta+ \csc\theta\cos\theta\cot\theta$

At this point, simplify using known Pythagorean identities. The left quantity simplifies such:

$\csc\theta\sin\theta = \frac{\sin\theta }{\sin\theta } = 1$

and the right quantity simplifies such:

$\csc\theta\cos\theta\cot\theta = (\frac{1}{\sin\theta })(\cos\theta )(\frac{\cos\theta }{\sin\theta })=\frac{\cos^{2}\theta }{\sin^{2}\theta }=\cot^{2}\theta$