How to find the area of a triangle - SSAT Elementary Level Quantitative

Card 0 of 120

You can find the area of a triangle if you know .

Tap to see back →

$Area _{\Delta } = $\frac{1}{2}$\times base \times height$

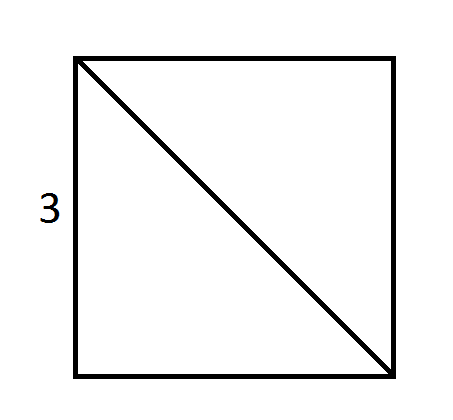
The square shown above has a side length of 3 and is divided into two triangles by its diagonal. What is the area of one of the triangles?

Tap to see back →

The area of the square is side times side, $3\times3=9$ .

Each triangle is half of the square, $9\div2=4.5$ .

What is the area of the triangle?

Tap to see back →

The formula to find the area of a triangle is $\frac{base \times height}{2}$ .

$A = $\frac{6\times 8}{2}$=24$

An isosceles triangle has a base of 12 cm and a height of 6 cm. What is the area of the triangle?

Tap to see back →

To find the area of a triangle, you must multiply $\frac{1}{2}$ by the base (12 cm) by the height (6 cm):

$\frac{12: cm}{2}$\times6 : cm=36: $cm^{2}$

Therefore the area of this triangle is $36: $cm^{2}$$ .

What is the area of the triangle?

Tap to see back →

The formula to find the area of a triangle is

$\frac{base \times height}{2}$

First, we should multiply (base) $\times$ (height), to get a total of .

Next, we need to divide by , which gives us a total area of .

Why is this shape a triangle?

Tap to see back →

A triangle has sides.

Why is this shape NOT a triangle?

Tap to see back →

A triangle has sides, and this shape has .

What two shapes can you find in this shape?

Tap to see back →

Find the area of a triangle with base 4 and height 7.

Tap to see back →

To solve, simply use the formula for the area of a triangle. Thus,

$A=\frac{1}{2}$Bh=\frac{1}{2}$47=\frac{1}{2}$*28=14$

To remember this formula, simply realize that two triangles added together would leave you with a rectangle, so a triangle's area must be half the area of a rectangle.

Find the area of the triangle shown below:

Tap to see back →

The area of a triangle can be expressed by the formula

$\frac{b\times h}{2}$ ,

or base times height divided by 2.

$$\frac{4\times12}{2}$=24$ .

If a triangle has a base of 3 inches and a height of 8 inches, what is the area of the triangle?

Tap to see back →

The formula for the area of a triangle is $$\frac{1}{2}$ \times base \times height= area$ .

Plug in the values given to solve the equation:

$$\frac{1}{2}$(3;in)(8;in)=$

$\frac{1}{2}$\times 3;in \times 8;in = $$\frac{1}{2}$;\times24;in^{2}$$=12;in^2$

The altitude of a triangle is given as , and its base as . What is the area of the triangle?

Tap to see back →

The area of a triangle is given by $0.5\times altitude\times base$ .

altitude

base $= 3\times a$ =

Therefore:

Area $= 0.5\times10\times30 = 150$

A triangle has a base of 10 centimeters and a height of 12 centimeters. What is the area of the triangle?

Tap to see back →

The formula for the area of a triangle is $area=\frac{1}{2}$(base)(height)$ .

Plug in the given values to solve for the area:

$$\frac{1}{2}$\times10cm\times12cm$

= $5cm\times12cm$

=

The area of this triangle is .

A triangle has a base of 14 and a height of 8. What is the area of the triangle?

Tap to see back →

To find the area of a triangle, multiply the base (14) by the height (8) and divide by 2:

$$\frac{14}{2}$\times8=56$

Therefore the area of this triangle is .

What is the area of a triangle with a base of 11 and a height of 4?

Tap to see back →

The formula to find the area of a triangle is $\frac{base \cdot height}{2}$ . First, we should multiply 11 (base) x 4 (height), to get a total of 44. Next, we need to divide 44 by 2, which gives us a total area of 22.

What is the area of the triangle in the figure?

Tap to see back →

Because the question asks you to find the AREA of the triangle, you are looking to figure out how much space the triangle covers. You find the area of triangles by multiplying the height of the triangle times the base and dividing by . So $A = 1/2 \times B \times H$ , or $A = 10 : cm \times 30 : cm \times 1/2$ . Therefore the correct answer is

A triangle has base of length units and a height of length units. What is the area of this triangle?

Tap to see back →

To calculate the area of a triangle, you use the formula $$\frac{1}{2}$\cdot b\cdot h$ , where is the length of the base of the triangle and is the height of the triangle. For this triangle, we need to solve the equation $$\frac{1}{2}$\cdot 6 \cdot 8$ to find its area. $6\cdot 8=48$ and $48\div2=24$ , so the triangle's area is units squared.

What is the area of a right triangle with a base of length 4 and a height that is 3 times longer than the base?

Tap to see back →

The area of a triangle is given by the formula $A = $\frac{1}{2}$\times b \times h$ , where is the length of the base and is the height.

First let's figure out the height. The base is 4, and the height is 3 times greater than the base:

$3 \times 4 = 12$

Now plug the base and height into the area formula:

$A = 0.5 \times 4 \times 12 = 2 \times 12 = 24$

The area of the triangle is 24.

The base of a triangle is , and the height is . What is the area of the triangle?

Tap to see back →

Write the formula for area of a triangle. Substitute the dimensions.

$A=\frac{bh}{2}$ = $\frac{(12)(20)}{2}$ = 12(10)=120$

The base of a triangle is and the height of the triangle is . What is the area of the triangle?

Tap to see back →

Write the formula for the area of a triangle.

$A=\frac{1}{2}$\times \textup{ Base }\times \textup{ Height}$

Substitute the base and height into the formula.

$A= $\frac{1}{2}$ (8)(3) = 12$