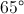How to find an angle in an acute / obtuse triangle

Help Questions

SSAT Upper Level Quantitative › How to find an angle in an acute / obtuse triangle

Questions 1 - 10

Find the angle measurement of .

Explanation

All the angles in a triangle must add up to .

The interior angles of a triangle measure $x^{\circ } , \left ( x+ 26\right )^{\circ } , \left (2x+ 1\right )^{\circ }$ . Of these three degree measures, give the greatest.

$77\frac{1}{2} ^{\circ }$

$64\frac{1}{4} ^{\circ }$

$77^{\circ }$

$103^{\circ }$

This triangle cannot exist.

Explanation

The degree measures of the interior angles of a triangle total 180 degrees, so

$\frac{4x}{4} = \frac{153}{4}$

$x = 38 \frac{1}{4}$

One angle measures $38\frac{1}{4}^{\circ }$

The other two angles measure

$x+ 26 = 38\frac{1}{4} + 26 = 64\frac{1}{4} ^{\circ }$

and

$2x+ 1 = 2 \left$38\frac{1}{4}\right$+ 1 = 77 \frac{1}{2} ^{\circ }$ .

We want the greatest of the three, or $77 \frac{1}{2} ^{\circ }$ .

If the vertex angle of an isoceles triangle is $64^{\circ}$ , what is the value of one of its base angles?

$58^{\circ}$

$116^{\circ}$

$64^{\circ}$

$36^{\circ}$

$26^{\circ}$

Explanation

In an isosceles triangle, the base angles are the same. Also, the three angles of a triangle add up to $180^{\circ}$ .

So, subtract the vertex angle from $180^{\circ}$ . You get $116^{\circ}$ .

Because there are two base angles you divide $116^{\circ}$ by , and you get $58^{\circ}$ .

Triangle

Note: Figure NOT drawn to scale.

Refer to the above diagram.

$45^{\circ } \leq m \angle 1 \leq 50^{\circ }$

$60^{\circ } \leq m \angle 2 \leq 70 ^{\circ }$

Which of the following could be a measure of $\angle 3$ ?

$110^{\circ }$

$100^{\circ }$

$125^{\circ }$

$130^{\circ }$

All of the other choices give a possible measure of $\angle 3$ .

Explanation

The measure of an exterior angle of a triangle is the sum of the measures of its remote interior angles, so

$\angle 3 = \angle 1 + \angle 2$ .

We also have the following constraints:

$45^{\circ } \leq m \angle 1 \leq 50^{\circ }$

$60^{\circ } \leq m \angle 2 \leq 70 ^{\circ }$

Then, by the addition property of inequalities,

$45^{\circ } + 60 ^{\circ }\leq m \angle 1 +m \angle 2 \leq 50^{\circ } + 70 ^{\circ }$

$105 ^{\circ }\leq m \angle 3 \leq 120^{\circ }$

Therefore, the measure of $\angle 3$ must fall in that range. Of the given choices, only $110^{\circ }$ falls in that range.

$\bigtriangleup ABC$ is a right triangle with right angle $\angle A$ . is located on $\overline{AB}$ so that, when $\overline{CD}$ is constructed, isosceles triangles $\bigtriangleup ADC$ and $\bigtriangleup BDC$ are formed.

What is the measure of $\angle B$ ?

$22\frac{1}{2}^{\circ }$

$45^{\circ }$

$67\frac{1}{2}^{\circ }$

$15^{\circ }$

$30^{\circ }$

Explanation

The figure referenced is below:

Right triangles

Since $\bigtriangleup ADC$ is an isosceles right triangle, its acute angles - in particular, $\angle ADC$ - measure $45^{\circ }$ each. Since this angle forms a linear pair with $\angle CDB$ :

$m \angle CDB = 180^{\circ } - m \angle ADC = 180^{\circ } - 45 ^{\circ } = 135^{\circ }$ .

$\bigtriangleup BDC$ is also isosceles, so, by the Isosceles Triangle Theorem, it has two congruent angles. Since $\angle CDB$ is obtuse, and no triangle has two obtuse angles:

$m \angle BCD = m \angle B$ .

Also, $\angle ADC$ is an exterior angle of $\bigtriangleup BDC$ , whose measure is equal to the sum of those of its two remote interior angles, which are the congruent angles $m \angle BCD = m \angle B$ . Therefore,

$m \angle ADC = m \angle BCD + m \angle B$

$45^{\circ }= m \angle B + m \angle B$

$45^{\circ }=2 m \angle B$

$m \angle B = 22\frac{1}{2}^{\circ }$

An isosceles triangle has an angle whose measure is $70^{\circ }$ .

What could be the measures of one of its other angles?

(a) $40^{\circ }$

(b) $55^{\circ }$

(a), (b), or (c)

(a) only

(b) only

(a) or (c) only

Explanation

By the Isosceles Triangle Theorem, an isosceles triangle has two congruent interior angles. There are two possible scenarios if one angle has measure $70^{\circ }$ :

Scenario 1: The other two angles are congruent to each other. The degree measures of the interior angles of a triangle total $180^{\circ }$ , so if we let be the common measure of those angles:

This makes (b) a possible answer.

Scenario 2: One of the other angles measures $70^{\circ }$ also, making (c) a possible answer. The degree measure of the third angle is

making (a) a possible answer. Therefore, the correct choice is (a), (b), or (c).

One of the interior angles of a scalene triangle measures $54^{\circ }$ . Which of the following could be the measure of another of its interior angles?

$108^{\circ }$

$126^{\circ }$

$63^{\circ }$

$54^{\circ }$

$72^{\circ }$

Explanation

A scalene triangle has three sides of different measure, so, by way of the Converse of the Isosceles Triangle Theorem, each angle is of different measure as well. We can therefore eliminate $54^{\circ }$ immediately.

Also, if the triangle also has a $72^{\circ }$ angle, then, since the total of the degree measures of the angles is $180^{\circ }$ , it follows that the third angle has measure

$180 - (54+72) = 180 - 126 = 54 ^{\circ }$ .

Therefore, the triangle has two angles that measure the same, and $72^{\circ }$ can be eliminated.

Similarly, if the triangle also has a $63^{\circ }$ angle, then, since the total of the degree measures of the angles is $180^{\circ }$ , it follows that the third angle has measure

$180 - (54+63) = 180 - 117= 63 ^{\circ }$ .

The triangle has two angles that measure $63^{\circ }$ . This choice can be eliminated.

$126^{\circ }$ can be eliminated, since the third angle would have measure

$180 - (54+126) = 180 - 180= 0^{\circ }$ ,

an impossible situation since angle measures must be positive.

The remaining possibility is $108^{\circ }$ . This would mean that the third angle has measure

$180 - (54+108) = 180 - 162= 18^{\circ }$ .

The three angles have different measures, so the triangle is scalene. $108^{\circ }$ is the correct choice.

Given: $\bigtriangleup ABC$ with $m \angle A = 20^{\circ }, m \angle B = 32^{\circ }$ . Locate on $\overline{AB}$ so that $\overrightarrow{CD}$ is the angle bisector of $\angle ACB$ . What is $m \angle CDB$ ?

$84^{\circ }$

$74^{\circ }$

$79^{\circ }$

$69^{\circ }$

$89^{\circ }$

Explanation

Angle bisector

Above is the figure described.

The measures of the interior angles of a triangle total $180^{\circ }$ , so the measure of $\angle ACB$ is

$m \angle ACB = 180^{\circ } -( m \angle A + m \angle B)$

$= 180^{\circ } -( 20^{\circ } + 32^{\circ })$

$= 180^{\circ } - 52^{\circ }$

$= 128^{\circ }$

Since $\overrightarrow{CD}$ bisects this angle,

$m \angle BCD= \frac{1}{2}m \angle ACB = \frac{1}{2} \cdot 128^{\circ } =64^{\circ }$

and

$m \angle CDB = 180^{\circ } -( m \angle BCD + m \angle B)$

$= 180^{\circ } -( 64 ^{\circ } + 32^{\circ } )$

$= 180^{\circ } -96^{\circ }$

$= 84^{\circ }$

Given: $\bigtriangleup ABC$ with $m \angle B = 74^{\circ }$ . is located on $\overline{AB}$ so that $\overrightarrow{CD}$ bisects $\angleACB$ $\angle ACB$ and forms isosceles triangle $\bigtriangleup BCD$ .

Give the measure of $\angle A$ .

$42^{\circ }$

Insufficient information is given to answer the question.

$64^{\circ }$

$74^{\circ }$

$53^{\circ }$

Explanation

If $\bigtriangleup BCD$ is isosceles, then by the Isosceles Triangle Theorem, two of its angles must be congruent.

Case 1: $m \angle B = m \angle BCD= 74^{\circ }$

Since $\overrightarrow{CD}$ bisects $\angleACB$ $\angle ACB$ into two congruent angles, one of which must be $m \angle BCD$ ,

$m \angle ACB = 2 \cdot m \angle BCD = 2 \cdot 74^{\circ } = 148^{\circ }$

However, this is impossible, since $\angle ACB$ and $\angle B$ are two angles of the original triangle; their total measure is

$m \angle ACB+ m \angle B = 148^{\circ }+ 74 ^{\circ } = 222 ^{\circ } > 180 ^{\circ }$

Case 2: $m \angle B = m \angle BDC= 74^{\circ }$

Then, since the degree measures of the interior angles of a triangle total $180^{\circ }$ ,

$m \angle BCD= 180^{\circ } - ( \angle B + m \angle BDC )$

$= 180^{\circ } - (74^{\circ } + 74^{\circ } )$

$= 180 ^{\circ } - 148^{\circ }$

$= 32^{\circ }$

Since $\overrightarrow{CD}$ bisects $\angleACB$ $\angle ACB$ into two congruent angles, one of which must be $m \angle BCD$ ,

$m \angle ACB = 2 \cdot m \angle BCD = 2 \cdot 32^{\circ } = 64^{\circ }$

and

$m \angle A = 180^{\circ } - ( \angle B + m \angle ACB )$

$= 180^{\circ } - (74^{\circ } + 64^{\circ } )$

$= 180^{\circ } - 138^{\circ }$

$= 42^{\circ }$

Case 3: $m \angle BDC= m \angle BCD$

Then

$m \angle B = 180^{\circ } -(m \angle BDC+ m \angle BCD)$

$74= 180^{\circ } -(m \angle BCD+ m \angle BCD)$

$74= 180^{\circ } -2 \cdot m \angle BCD$

$2 \cdot m \angle BCD = 106^{\circ }$

$m \angle BCD = 53^{\circ }$

$m \angle ACB = 2 \cdot m \angle BCD = 2 \cdot 53^{\circ } = 106^{\circ }$

$m \angle A = 180^{\circ } - ( \angle B + m \angle ACB )$

$= 180^{\circ } - ( 74^{\circ }+ 106^{\circ } )$

$= 0^{\circ }$ , which is not possible.

Therefore, the only possible measure of $\angle A$ is $42^{\circ }$ .

Triangle_a

Figure NOT drawn to scale.

If $x = 72^{\circ }$ and $y = 43^{\circ }$ , evaluate .

$115^{\circ }$

$125^{\circ }$

$108^{\circ}$

$65^{\circ}$

$137^{\circ}$

Explanation

The measure of an exterior angle of a triangle is the sum of the measures of its remote interior angles, so

$w = x + y = 72 + 43 = 115 ^{\circ }$

Page 1 of 2

Return to subject

AI TutorYour personal study buddy

Question of the DayDaily practice to build your skills

FlashcardsStudy and memorize key concepts

WorksheetsBuild custom practice quizzes

AI SolverStep-by-step problem solutions

Learn by ConceptMaster concepts step by step

Diagnostic TestsAssess your knowledge level

Practice TestsTest your skills with exam questions

GamesLearn through free games