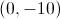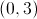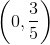How to find x or y intercept
Help Questions
SSAT Upper Level Quantitative › How to find x or y intercept
Define 




Explanation
An 






Substituting the definition, we get
Solving for 
The 


To determine which of the four choices is correct, substitute 





The correct choice is 
Define a function 


(a)
(b)
Neither (a) nor (b)
Both (a) and (b)
(b), but not (a)
(a), but not (b)
Explanation
An 






We can most easily determine whether 






Similarly, substituting 3 for 



Define a function 


Explanation
The 





The correct choice is 
Give the 


The line has no 
Explanation
By the point-slope formula, this line has the equation
where
By substitution, the equation becomes
To find the 


The 

What is the 
The graph has no 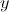
Explanation
The 




The 

Give the 
The graph has no 
Explanation
The 




However, since this expression has 0 in a denominator, it is of undefined value. This means that there is no value of 


What is the 

Explanation
The 




The 

Give the 
The graph has no 
Explanation
The 




The 

Give the 

The graph does not have a 
Explanation
The 




The 

A line passes through 


The line has no 
Explanation
First, find the slope of the second line 

The equation is now in the slope-intercept form 


The first line, being perpendicular to the second, has as its slope the opposite of the reciprocal of 

Therefore, we are looking for a line through 

with

the equation becomes

To find the 


The