Phase Shifts - Trigonometry
Card 0 of 32
Which of the following is equivalent to 
Which of the following is equivalent to
Tap to see back →
The first zero can be found by plugging 3π/2 for x, and noting that it is a double period function, the zeros are every π/2, count three back and there is a zero at zero, going down.
A more succinct form for this answer is  but that was not one of the options, so a shifted cosine must be the answer.
but that was not one of the options, so a shifted cosine must be the answer.
The first positive peak is at π/4 at -1, so the cosine function will be shifted π/4 to the right and multiplied by -1. The period and amplitude still 2, so the answer becomes  .
.
To check, plug in π/4 for x and it will come out to -2.
The first zero can be found by plugging 3π/2 for x, and noting that it is a double period function, the zeros are every π/2, count three back and there is a zero at zero, going down.
A more succinct form for this answer is 
The first positive peak is at π/4 at -1, so the cosine function will be shifted π/4 to the right and multiplied by -1. The period and amplitude still 2, so the answer becomes 
To check, plug in π/4 for x and it will come out to -2.
Identify the phase shift of the following equation.

Identify the phase shift of the following equation.
Tap to see back →
If we use the standard form of a sine function
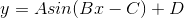
the phase shift can be calculated by  . Therefore, in our case, our phase shift is
. Therefore, in our case, our phase shift is


If we use the standard form of a sine function
the phase shift can be calculated by 
Which of the following is the correct definition of a phase shift?
Which of the following is the correct definition of a phase shift?
Tap to see back →
Take the function  for example. The graph for
for example. The graph for  is
is
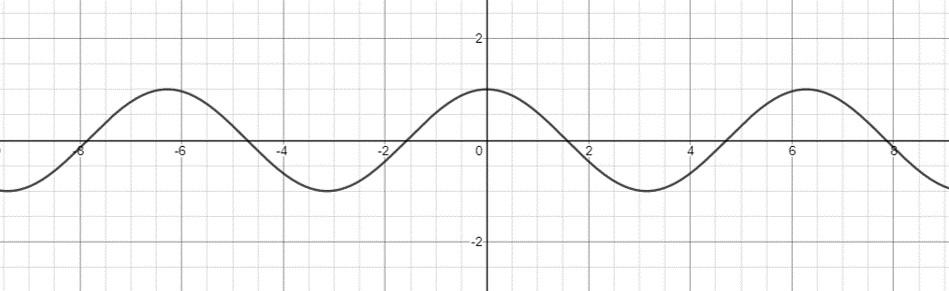
If we were to change the function to  , our phase shift is
, our phase shift is  . This means we need to shift our entire graph
. This means we need to shift our entire graph  units to the left.
units to the left.
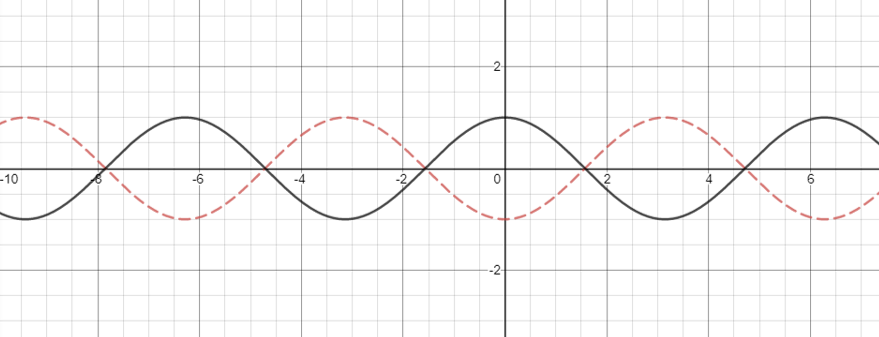
Our new graph  is the following
is the following

Take the function 

If we were to change the function to 


Our new graph 
Consider the function  . What is the phase shift of this function?
. What is the phase shift of this function?
Consider the function 
Tap to see back →
The general form for the secant transformation equation is  .
.  represents the phase shift of the function. When considering
represents the phase shift of the function. When considering  we see that
we see that  . So our phase shift is
. So our phase shift is  and we would shift this function
and we would shift this function  units to the left of the original secant function’s graph.
units to the left of the original secant function’s graph.
The general form for the secant transformation equation is 





True or False: If the function  has a phase shift of
has a phase shift of  , then the graph will not be changed.
, then the graph will not be changed.
True or False: If the function 

Tap to see back →
Which of the following is the graph of  with a phase shift of
with a phase shift of  ?
?
Which of the following is the graph of 

Tap to see back →
Start this problem by graphing the function of tangent.

Now we need to shift this graph  to the right.
to the right.

This gives us our answer

Start this problem by graphing the function of tangent.

Now we need to shift this graph 

This gives us our answer

True or False: The function  has a phase shift of
has a phase shift of  .
.
True or False: The function 

Tap to see back →
The form of the general cosecant function is  . So if we have
. So if we have  then
then  , which represents the phase shift, is equal to
, which represents the phase shift, is equal to  . This gives us a phase shift of
. This gives us a phase shift of  .
.
The form of the general cosecant function is 




Which of the following is the phase shift of the function  ?
?
Which of the following is the phase shift of the function 
Tap to see back →
The general form of the cotangent function is  . So first we need to get
. So first we need to get  into the form
into the form  .
.


From this we see that  giving us our answer.
giving us our answer.
The general form of the cotangent function is 


From this we see that 
Which of the following is equivalent to 
Which of the following is equivalent to
Tap to see back →
The first zero can be found by plugging 3π/2 for x, and noting that it is a double period function, the zeros are every π/2, count three back and there is a zero at zero, going down.
A more succinct form for this answer is  but that was not one of the options, so a shifted cosine must be the answer.
but that was not one of the options, so a shifted cosine must be the answer.
The first positive peak is at π/4 at -1, so the cosine function will be shifted π/4 to the right and multiplied by -1. The period and amplitude still 2, so the answer becomes  .
.
To check, plug in π/4 for x and it will come out to -2.
The first zero can be found by plugging 3π/2 for x, and noting that it is a double period function, the zeros are every π/2, count three back and there is a zero at zero, going down.
A more succinct form for this answer is 
The first positive peak is at π/4 at -1, so the cosine function will be shifted π/4 to the right and multiplied by -1. The period and amplitude still 2, so the answer becomes 
To check, plug in π/4 for x and it will come out to -2.
Identify the phase shift of the following equation.

Identify the phase shift of the following equation.
Tap to see back →
If we use the standard form of a sine function
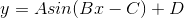
the phase shift can be calculated by  . Therefore, in our case, our phase shift is
. Therefore, in our case, our phase shift is


If we use the standard form of a sine function
the phase shift can be calculated by 
Which of the following is the correct definition of a phase shift?
Which of the following is the correct definition of a phase shift?
Tap to see back →
Take the function  for example. The graph for
for example. The graph for  is
is

If we were to change the function to  , our phase shift is
, our phase shift is  . This means we need to shift our entire graph
. This means we need to shift our entire graph  units to the left.
units to the left.

Our new graph  is the following
is the following

Take the function 

If we were to change the function to 


Our new graph 
Consider the function  . What is the phase shift of this function?
. What is the phase shift of this function?
Consider the function 
Tap to see back →
The general form for the secant transformation equation is  .
.  represents the phase shift of the function. When considering
represents the phase shift of the function. When considering  we see that
we see that  . So our phase shift is
. So our phase shift is  and we would shift this function
and we would shift this function  units to the left of the original secant function’s graph.
units to the left of the original secant function’s graph.
The general form for the secant transformation equation is 





True or False: If the function  has a phase shift of
has a phase shift of  , then the graph will not be changed.
, then the graph will not be changed.
True or False: If the function 

Tap to see back →
Which of the following is the graph of  with a phase shift of
with a phase shift of  ?
?
Which of the following is the graph of 

Tap to see back →
Start this problem by graphing the function of tangent.

Now we need to shift this graph  to the right.
to the right.

This gives us our answer

Start this problem by graphing the function of tangent.

Now we need to shift this graph 

This gives us our answer

True or False: The function  has a phase shift of
has a phase shift of  .
.
True or False: The function 

Tap to see back →
The form of the general cosecant function is  . So if we have
. So if we have  then
then  , which represents the phase shift, is equal to
, which represents the phase shift, is equal to  . This gives us a phase shift of
. This gives us a phase shift of  .
.
The form of the general cosecant function is 




Which of the following is the phase shift of the function  ?
?
Which of the following is the phase shift of the function 
Tap to see back →
The general form of the cotangent function is  . So first we need to get
. So first we need to get  into the form
into the form  .
.


From this we see that  giving us our answer.
giving us our answer.
The general form of the cotangent function is 


From this we see that 
Which of the following is equivalent to 
Which of the following is equivalent to
Tap to see back →
The first zero can be found by plugging 3π/2 for x, and noting that it is a double period function, the zeros are every π/2, count three back and there is a zero at zero, going down.
A more succinct form for this answer is  but that was not one of the options, so a shifted cosine must be the answer.
but that was not one of the options, so a shifted cosine must be the answer.
The first positive peak is at π/4 at -1, so the cosine function will be shifted π/4 to the right and multiplied by -1. The period and amplitude still 2, so the answer becomes  .
.
To check, plug in π/4 for x and it will come out to -2.
The first zero can be found by plugging 3π/2 for x, and noting that it is a double period function, the zeros are every π/2, count three back and there is a zero at zero, going down.
A more succinct form for this answer is 
The first positive peak is at π/4 at -1, so the cosine function will be shifted π/4 to the right and multiplied by -1. The period and amplitude still 2, so the answer becomes 
To check, plug in π/4 for x and it will come out to -2.
Identify the phase shift of the following equation.

Identify the phase shift of the following equation.
Tap to see back →
If we use the standard form of a sine function
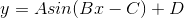
the phase shift can be calculated by  . Therefore, in our case, our phase shift is
. Therefore, in our case, our phase shift is


If we use the standard form of a sine function
the phase shift can be calculated by 
Which of the following is the correct definition of a phase shift?
Which of the following is the correct definition of a phase shift?
Tap to see back →
Take the function  for example. The graph for
for example. The graph for  is
is

If we were to change the function to  , our phase shift is
, our phase shift is  . This means we need to shift our entire graph
. This means we need to shift our entire graph  units to the left.
units to the left.

Our new graph  is the following
is the following

Take the function 

If we were to change the function to 


Our new graph 
Consider the function  . What is the phase shift of this function?
. What is the phase shift of this function?
Consider the function 
Tap to see back →
The general form for the secant transformation equation is  .
.  represents the phase shift of the function. When considering
represents the phase shift of the function. When considering  we see that
we see that  . So our phase shift is
. So our phase shift is  and we would shift this function
and we would shift this function  units to the left of the original secant function’s graph.
units to the left of the original secant function’s graph.
The general form for the secant transformation equation is 





 has a period of
has a period of  , meaning it repeats itself every
, meaning it repeats itself every  units. So if
units. So if  has a phase shift of any multiple of
has a phase shift of any multiple of  and in purple is the graph of
and in purple is the graph of  .
.
