Vectors - Trigonometry
Card 0 of 32
Determine the magnitude of vector A.

Determine the magnitude of vector A.
Tap to see back →
We can use the pythagorean theorem to solve this problem. Using  as our hypotenuse, we can drop a vertical vector perpendicular to the x-axis. We will call this
as our hypotenuse, we can drop a vertical vector perpendicular to the x-axis. We will call this  and it is 4 units in length. We can also extend a vector from the origin that connects to
and it is 4 units in length. We can also extend a vector from the origin that connects to  . We will call this
. We will call this  and it is 3 units in length.
and it is 3 units in length.
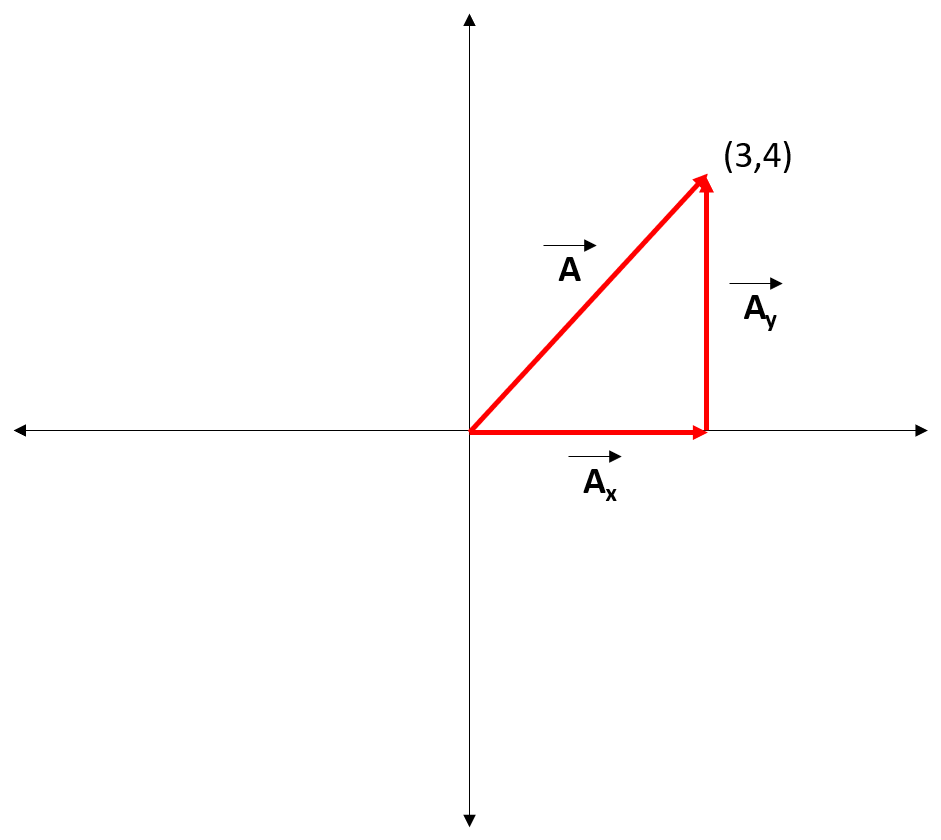
Using the pythagorean theorem:






We can use the pythagorean theorem to solve this problem. Using 



Using the pythagorean theorem:
Which of the following is the correct term for the sum of two vectors?
Which of the following is the correct term for the sum of two vectors?
Tap to see back →
When summing two vectors, you have both an x and y component and you sum these separately leaving you with a coordinate as your answer. This coordinate is called a resultant.
When summing two vectors, you have both an x and y component and you sum these separately leaving you with a coordinate as your answer. This coordinate is called a resultant.
Determine the resultant of  and
and  .
.
Determine the resultant of 

Tap to see back →
When determining the resultant of two vectors, you are finding the sum of two vectors. To do this you must add the x component and the y component separately.



When determining the resultant of two vectors, you are finding the sum of two vectors. To do this you must add the x component and the y component separately.
Consider the following graphs where  begins at the origin and ends at
begins at the origin and ends at  and
and  . Which of the following depicts the correct resultant of these two vectors.
. Which of the following depicts the correct resultant of these two vectors.

Consider the following graphs where 



Tap to see back →
To find the resultant we must sum the two vectors:



Now we must graph the resultant

To find the resultant we must sum the two vectors:
Now we must graph the resultant

How many degrees above the x-axis is  ?
?

How many degrees above the x-axis is 

Tap to see back →
First, we must understand what we are solving for. We are solving for the angle that is formed by  and the x-axis. To do this, we can extend a vector from the origin which stops directly under the end of
and the x-axis. To do this, we can extend a vector from the origin which stops directly under the end of  . We will call this new vector
. We will call this new vector  and it will be 7 units long. We will also extend a vector upwards that is perpendicular to the x-axis. We will call this
and it will be 7 units long. We will also extend a vector upwards that is perpendicular to the x-axis. We will call this  and it will be 3 units long.
and it will be 3 units long.

Now we can use the relationship that  where
where  is the adjacent side and
is the adjacent side and  is the opposite side.
is the opposite side.




And so  is 23.2 degrees above the x-axis.
is 23.2 degrees above the x-axis.
First, we must understand what we are solving for. We are solving for the angle that is formed by 




Now we can use the relationship that 


And so 
Find the difference of the two vectors,  which ends at
which ends at  and
and  ending at
ending at  .
.
Find the difference of the two vectors, 



Tap to see back →
When finding the difference of two vectors, you must subtract the x and y components separately.



When finding the difference of two vectors, you must subtract the x and y components separately.
Which of the following is the correct depiction of the difference of vectors A and B?

Which of the following is the correct depiction of the difference of vectors A and B?

Tap to see back →
To find the difference of two vectors we must consider the x and y components separately.



And then we must correctly graph this vector

To find the difference of two vectors we must consider the x and y components separately.
And then we must correctly graph this vector

True or False: The magnitude of a vector is the length of the vector.
True or False: The magnitude of a vector is the length of the vector.
Tap to see back →
When finding the magnitude of the vector, you use either the Pythagorean Theorem by forming a right triangle with the vector in question or you can use the distance formula. This is much more clear considering the distance vector that the magnitude of the vector is in fact the length of the vector.
When finding the magnitude of the vector, you use either the Pythagorean Theorem by forming a right triangle with the vector in question or you can use the distance formula. This is much more clear considering the distance vector that the magnitude of the vector is in fact the length of the vector.
Determine the magnitude of vector A.

Determine the magnitude of vector A.
Tap to see back →
We can use the pythagorean theorem to solve this problem. Using  as our hypotenuse, we can drop a vertical vector perpendicular to the x-axis. We will call this
as our hypotenuse, we can drop a vertical vector perpendicular to the x-axis. We will call this  and it is 4 units in length. We can also extend a vector from the origin that connects to
and it is 4 units in length. We can also extend a vector from the origin that connects to  . We will call this
. We will call this  and it is 3 units in length.
and it is 3 units in length.

Using the pythagorean theorem:






We can use the pythagorean theorem to solve this problem. Using 



Using the pythagorean theorem:
Which of the following is the correct term for the sum of two vectors?
Which of the following is the correct term for the sum of two vectors?
Tap to see back →
When summing two vectors, you have both an x and y component and you sum these separately leaving you with a coordinate as your answer. This coordinate is called a resultant.
When summing two vectors, you have both an x and y component and you sum these separately leaving you with a coordinate as your answer. This coordinate is called a resultant.
Determine the resultant of  and
and  .
.
Determine the resultant of 

Tap to see back →
When determining the resultant of two vectors, you are finding the sum of two vectors. To do this you must add the x component and the y component separately.



When determining the resultant of two vectors, you are finding the sum of two vectors. To do this you must add the x component and the y component separately.
Consider the following graphs where  begins at the origin and ends at
begins at the origin and ends at  and
and  . Which of the following depicts the correct resultant of these two vectors.
. Which of the following depicts the correct resultant of these two vectors.

Consider the following graphs where 



Tap to see back →
To find the resultant we must sum the two vectors:



Now we must graph the resultant

To find the resultant we must sum the two vectors:
Now we must graph the resultant

How many degrees above the x-axis is  ?
?

How many degrees above the x-axis is 

Tap to see back →
First, we must understand what we are solving for. We are solving for the angle that is formed by  and the x-axis. To do this, we can extend a vector from the origin which stops directly under the end of
and the x-axis. To do this, we can extend a vector from the origin which stops directly under the end of  . We will call this new vector
. We will call this new vector  and it will be 7 units long. We will also extend a vector upwards that is perpendicular to the x-axis. We will call this
and it will be 7 units long. We will also extend a vector upwards that is perpendicular to the x-axis. We will call this  and it will be 3 units long.
and it will be 3 units long.

Now we can use the relationship that  where
where  is the adjacent side and
is the adjacent side and  is the opposite side.
is the opposite side.




And so  is 23.2 degrees above the x-axis.
is 23.2 degrees above the x-axis.
First, we must understand what we are solving for. We are solving for the angle that is formed by 




Now we can use the relationship that 


And so 
Find the difference of the two vectors,  which ends at
which ends at  and
and  ending at
ending at  .
.
Find the difference of the two vectors, 



Tap to see back →
When finding the difference of two vectors, you must subtract the x and y components separately.



When finding the difference of two vectors, you must subtract the x and y components separately.
Which of the following is the correct depiction of the difference of vectors A and B?

Which of the following is the correct depiction of the difference of vectors A and B?

Tap to see back →
To find the difference of two vectors we must consider the x and y components separately.



And then we must correctly graph this vector

To find the difference of two vectors we must consider the x and y components separately.
And then we must correctly graph this vector

True or False: The magnitude of a vector is the length of the vector.
True or False: The magnitude of a vector is the length of the vector.
Tap to see back →
When finding the magnitude of the vector, you use either the Pythagorean Theorem by forming a right triangle with the vector in question or you can use the distance formula. This is much more clear considering the distance vector that the magnitude of the vector is in fact the length of the vector.
When finding the magnitude of the vector, you use either the Pythagorean Theorem by forming a right triangle with the vector in question or you can use the distance formula. This is much more clear considering the distance vector that the magnitude of the vector is in fact the length of the vector.
Determine the magnitude of vector A.

Determine the magnitude of vector A.
Tap to see back →
We can use the pythagorean theorem to solve this problem. Using  as our hypotenuse, we can drop a vertical vector perpendicular to the x-axis. We will call this
as our hypotenuse, we can drop a vertical vector perpendicular to the x-axis. We will call this  and it is 4 units in length. We can also extend a vector from the origin that connects to
and it is 4 units in length. We can also extend a vector from the origin that connects to  . We will call this
. We will call this  and it is 3 units in length.
and it is 3 units in length.

Using the pythagorean theorem:






We can use the pythagorean theorem to solve this problem. Using 



Using the pythagorean theorem:
Which of the following is the correct term for the sum of two vectors?
Which of the following is the correct term for the sum of two vectors?
Tap to see back →
When summing two vectors, you have both an x and y component and you sum these separately leaving you with a coordinate as your answer. This coordinate is called a resultant.
When summing two vectors, you have both an x and y component and you sum these separately leaving you with a coordinate as your answer. This coordinate is called a resultant.
Determine the resultant of  and
and  .
.
Determine the resultant of 

Tap to see back →
When determining the resultant of two vectors, you are finding the sum of two vectors. To do this you must add the x component and the y component separately.



When determining the resultant of two vectors, you are finding the sum of two vectors. To do this you must add the x component and the y component separately.
Consider the following graphs where  begins at the origin and ends at
begins at the origin and ends at  and
and  . Which of the following depicts the correct resultant of these two vectors.
. Which of the following depicts the correct resultant of these two vectors.

Consider the following graphs where 



Tap to see back →
To find the resultant we must sum the two vectors:



Now we must graph the resultant

To find the resultant we must sum the two vectors:
Now we must graph the resultant






















