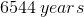In this question, we're given a brief description of radiocarbon dating. We're given the amount of \(\displaystyle C^{14}\) that has been found in a fossil sample and we're asked to find the approximate age of the fossil.

First, let's briefly go over radiocarbon dating. This method essentially assumes that the amount of radioactive carbon within an organism remains fairly stable at any given time while the organism is alive. Moreover, this amount of radioactive carbon is related to the amount of radioactive carbon in the atmosphere. Once the organism dies, however, it ceases to gain any radioactive carbon; rather, the \(\displaystyle C^{14}\) that was present now begins to decay into \(\displaystyle C^{12}\). Thus, by measuring the amount of \(\displaystyle C^{14}\) in the organism and comparing it to the amount in the atmosphere, the age at which the organism died can be approximated.

Since we're dealing with the decay of \(\displaystyle C^{14}\), this is a radioactive decay problem. Recall that all radioactive decay reactions follow first-order rate kinetics. What this means is that the rate of decay is only dependent on the amount of radioactive material at any given instant. Hence, we can use the first-order rate equation.

\(\displaystyle A_{t}=A_{0}e^{-kt}\)

We can further rearrange this expression to isolate the variable for time.

\(\displaystyle \frac{A_t}{A_0}=e^{-kt}\)

\(\displaystyle t=-\frac{ln(\frac{A_t}{A_0})}{k}\)

In arriving at this expression, we see that we need to know the rate constant, \(\displaystyle k\), in order to solve for \(\displaystyle t\). To do this, we can use the equation that relates the half-life to the rate constant for a first-order process.

\(\displaystyle t_\frac{1}{2}=\frac{ln(2)}{k}\)

Rearranging, we can find the rate-constant.

\(\displaystyle k=\frac{ln(2)}{t_\frac{1}{2}}\)

\(\displaystyle k=\frac{0.693}{5730\: yr}=1.21\cdot 10^{-4}\: yr^{-1}\)

Now that we have the rate constant, we can plug this value into the previous expression to solve for \(\displaystyle t\).

\(\displaystyle t=-\frac{ln(\frac{0.35}{1})}{1.21\cdot 10^{-4}\: yr^{-1}}=8676\:years\)

For this problem, the first step is to find the rate constant for the decay reaction. Since we're given the half-life, we can calculate this value using the following equation.

\(\displaystyle k=\frac{ln(2)}{t_{\frac{1}{2}}}\)

\(\displaystyle k=\frac{0.693}{20\:min}=0.03465\:min^{-1}\)

Now, we can use the first order rate equation to find out how much drug will be left after the first time interval of \(\displaystyle 15\) minutes.

\(\displaystyle A_{t}=A_{o}e^{-kt}\)

\(\displaystyle A_{15\:min}=(30\:mg)e^{-(0.03465\:min^{-1})(15\:min)}\)

\(\displaystyle A_{15\:min}=17.84\:mg\)

So, after the first \(\displaystyle 15\) minutes, there will be \(\displaystyle 17.84\:mg\) of the drug in the patient's body. But from the question stem we're told that an additional \(\displaystyle 25\:mg\) of the drug is injected. Hence, there is now \(\displaystyle 42.84\:mg\) of the drug present.

With this new amount in mind, we'll need to calculate how much of the drug will be present after more time has elapsed. We can do this by using the same equation as before.

\(\displaystyle A_{10\:min}=(42.84\:mg)e^{-(0.03465\:min^{-1})(10\:min)}\)

\(\displaystyle A_{10\:min}=30.29\:mg\)

This is the final amount of drug that is expected to be present in the patient's body at that instant of time.

Finding the amount is a simple half life problem. Start with setting up what you know for any half-life problem.

\(\displaystyle 100 = 200e^{i*8.02}\), \(\displaystyle i\) is the rate of decay, 200 is the initial amount, and 100 is the half left after 8.02 days.

From there simplify. 

\(\displaystyle 0.5 = e^{8.02 * i}\). To solve this take the natural log of both sides so that 

\(\displaystyle ln (0.5) = 8.02i\)

\(\displaystyle i=-0.086\)

Now plug this into the equation and find what happens after 7 days.

\(\displaystyle S = 200e^{-0.086*7}=109.2g\)

Beta decay is when a neutron releases an electron and becomes a proton. Therefore, the atomic number goes up by one but the atomic mass remains the same. This results in xenon-131.