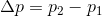All AP Physics B Resources
Example Questions
Example Question #1 : Understanding Conservation Of Momentum
A baseball pitcher throws a baseball at 


In order to calculate the change in momentum, we must find the initial and final momentum of the baseball, and then find the difference.
Use the given velocities and mass to calculate the initial and final values.
The initial momentum is positive because the problem states that the ball was originally thrown in the positive direction. The final momentum is negative due to the change in direction.
Now we find the change in momentum:
Example Question #51 : Mcat Physical Sciences
Ball A, traveling 

A perfectly inelastic collision is when the two bodies stick together at the end. At the beginning the two balls are traveling separately with individual momentum values. Using the momentum equation 
Note: ball B's velocity is negative because they are traveling in opposite directions.
The negative sign indicates the direction in which the two balls are traveling. Since the sign is negative and we indicated that traveling to the left is negative, the two balls must be traveling 2m/s to the left after the perfectly inelastic collision.
Example Question #1 : Momentum
Two astronauts, Ann and Bob, conduct a collision experiment in a weightless, frictionless environment. Initially Ann moves to the right with a momentum of 
to the left. What is Bob's final momentum?

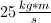




Apply conservation of momentum before and after the collision.

Taking left to be the negative direction, and noting that Bob's initial momentum is 0 since he is at rest, we can use the provided information to see that 
Solving for 

Example Question #2 : Momentum
A 










This is a completely inelastic collision, and, as with all collisions, it conserves linear momentum. To get magnitude and direction in two dimensions, it is typically best to look at the horizontal and vertical directions individually.
Horizontal direction: The 

The 

So the total x-momentum after the collision is the sum of these two initial x-momenta, since total momentum is conserved in the collision.
This immediately shows that the combined mass after the collision is moving in the positive x-direction.
We now need to compute the final velocity in the x-direction. In this case:


Vertical direction: The same procedure can be applied to the y-direction. In this case, the process is simpler, because only the 

Since the final momentum is now known to be positive in both the horizontal and vertical directions, the angle with respect to the x-axis must be positive. Now, the final y-direction velocity can be calculated.
Final velocity: With the final velocity components known, the final velocity can be calculated from trigonometry.
Magnitude:
Direction:
Certified Tutor
Certified Tutor
All AP Physics B Resources