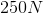College Physics : Newton's Laws and Fundamental Concepts
Study concepts, example questions & explanations for College Physics
All College Physics Resources
Example Questions
Example Question #1 : Forces
A juggler throws a ball straight up into the air, which exerts air resistance on the ball. Which of the following best describes the speed of the ball after it falls and just reaches the juggler's hand?
The speed of the ball is exactly the same as when it was released.
The speed of the ball is less than when the juggler first threw it.
The speed of the ball is greater than when it was released.
The speed of the ball is zero.
None of the other answers.
The speed of the ball is less than when the juggler first threw it.
Air resistance is like a friction force that takes energy away from the ball. Because the ball has energy taken from it on the way up and the way down, there is net negative work done on the ball. The energy of the ball is not conserved and it slows down slightly compared to when it was released.
Example Question #1 : Forces
A 
This is a simple case of 
Example Question #2 : Forces
A 
In this case, the rope must be able to support both the force of gravity and the force required to accelerate the block. Both are given by 
Example Question #3 : Forces
A 
Let's first write down the information we are given:
We know that 
Let's manipulate the equation by solving for velocity so we can simply plug in the numbers we are given:
so:
Example Question #3 : Forces
A 
Let's write down the information we are given:
We know that 
So we can just plug in the information we are given to solve for the Force:
Example Question #4 : Forces
An object is pushed from rest with a force of 
Let's write down the information we are given:
We know that 
So we can solve for 
Example Question #5 : Forces
An hourglass is placed on a scale with all its sand in the upper chamber. A short time later, the sand begins to fall into the lower chamber. Which of the following best describes the reading on the scale as a function of time before any sand has accumulated in the bottom chamber?
The reading on the scale stays the same.
The reading on the scale decreases slightly.
The reading on the scale is zero.
None of these
The reading on the scale increases.
The reading on the scale decreases slightly.
Initially, when all the sand is in the upper chamber, the reading on the scale is constant and corresponds to the weight of the hourglass and the sand within. As some sand falls, there is no normal force on it so the scale can not register its weight. The fraction of sand that is falling is small, so there is only a small decrease in the apparent weight of the hourglass.
Example Question #6 : Forces
A block which weighs 
Let's first write down the information we are given:
We know that 
Let's manipulate the equation by solving for time so we can simply plug in the numbers we are given:
so:
All College Physics Resources
