Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : How to find the ratio of diameter and circumference

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Ratio Of Diameter And Circumference

What is the ratio of the diameter of a circle to the circumference of the same circle?

Possible Answers:

$\frac{1}{\pi}$

$\frac{\pi}{C}$

$\pi$

$D\pi$

Correct answer:

$\frac{1}{\pi}$

Explanation:

To find the ratio we must know the equation for the circumference of a circle. In this equation, is the circumference and is the diameter.

$C=D\pi$

Once we know the equation, we can solve for the ratio of the diameter to circumference by solving the equation for $\frac{D}{C}$ . We do this by dividing both sides by .

$\frac{C}{\pi}=\frac{D\pi}{\pi}$

$\frac{C}{\pi}=D$

Then we divide both sides by the circumference.

$\frac{C}{\pi C}=\frac{1}{\pi}=\frac{D}{C}$

We now know that the ratio of the diameter to circumference is equal to $\frac{1}{\pi}$ .

Report an Error

Example Question #2 : How To Find The Ratio Of Diameter And Circumference

What is the ratio of the diameter and circumference of a circle?

Possible Answers:

$2\pi$

$\pi$

$\frac{\pi}{2}$

Correct answer:

Explanation:

To find the ratio we must know the equation for the circumference of a circle is

$Circumference=\pi d$

Once we know the equation we can solve for the ratio of the diameter to circumference by solving the equation for $\frac{diameter}{Circumference}$

we divide both sides by the circumference giving us

$\frac{d}{\pi d}=\frac{1}{\pi }$

We now know that the ratio of the diameter to circumference is equal to .

Report an Error

Example Question #1 : How To Find The Ratio Of Diameter And Circumference

Let represent the area of a circle and represent its circumference. Which of the following equations expresses in terms of ?

Possible Answers:

C^2

Correct answer:

Explanation:

The formula for the area of a circle is $A=\pi r^2$ , and the formula for circumference is $C=2\pi r$ . If we solve for C in terms of r, we get
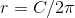
$r=C/2\pi$ .

We can then substitute this value of r into the formula for the area:

$A=\pi r^2$

$=\pi (C/2\pi )^2$

$=C^2\pi /4\pi ^2$

$=C^2/4\pi$

Report an Error

Example Question #1 : How To Find The Ratio Of Diameter And Circumference

What is the ratio of any circle's circumference to its radius?

Possible Answers:

$\pi ^{2}:1$

3.14:1

Undefined.

$2\pi :1$

$\pi :1$

Correct answer:

$2\pi :1$

Explanation:

The circumference of any circle is

$2\pi*r$

So the ratio of its circumference to its radius r, is

$\frac{2\pi*r}{r}$

$=2\pi$

Report an Error

View Tutors

Constance
Certified Tutor

Loyola University-Chicago, Bachelors, Psychology. Sam Houston State University, Masters, Counseling Psychology.

View Tutors

Anne
Certified Tutor

University of Maryland-Baltimore, Doctor of Science, Accounting.

View Tutors

Satweka
Certified Tutor

The University of Texas at Dallas, Master of Science, Biomedical Engineering.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Spanish Tutors in Miami, Biology Tutors in Houston, Reading Tutors in Dallas Fort Worth, Statistics Tutors in Washington DC, Calculus Tutors in Phoenix, Reading Tutors in Houston, Biology Tutors in Chicago, Spanish Tutors in Denver, Math Tutors in Denver, Chemistry Tutors in Atlanta

Popular Courses & Classes

ISEE Courses & Classes in Miami, MCAT Courses & Classes in San Francisco-Bay Area, GMAT Courses & Classes in San Diego, GRE Courses & Classes in Houston, GMAT Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Houston, Spanish Courses & Classes in Seattle, SSAT Courses & Classes in Denver, LSAT Courses & Classes in Philadelphia, SAT Courses & Classes in Atlanta

Popular Test Prep

LSAT Test Prep in Atlanta, LSAT Test Prep in Phoenix, LSAT Test Prep in Seattle, LSAT Test Prep in Miami, GRE Test Prep in San Diego, GRE Test Prep in Houston, SAT Test Prep in Boston, LSAT Test Prep in New York City, ACT Test Prep in Phoenix, SSAT Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : How to find the ratio of diameter and circumference

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : How To Find The Ratio Of Diameter And Circumference

Example Question #2 : How To Find The Ratio Of Diameter And Circumference

Example Question #1 : How To Find The Ratio Of Diameter And Circumference

Example Question #1 : How To Find The Ratio Of Diameter And Circumference

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: