We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Middle Level Math : How to find the area of a parallelogram

Study concepts, example questions & explanations for SSAT Middle Level Math

Create An Account

All SSAT Middle Level Math Resources

10 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

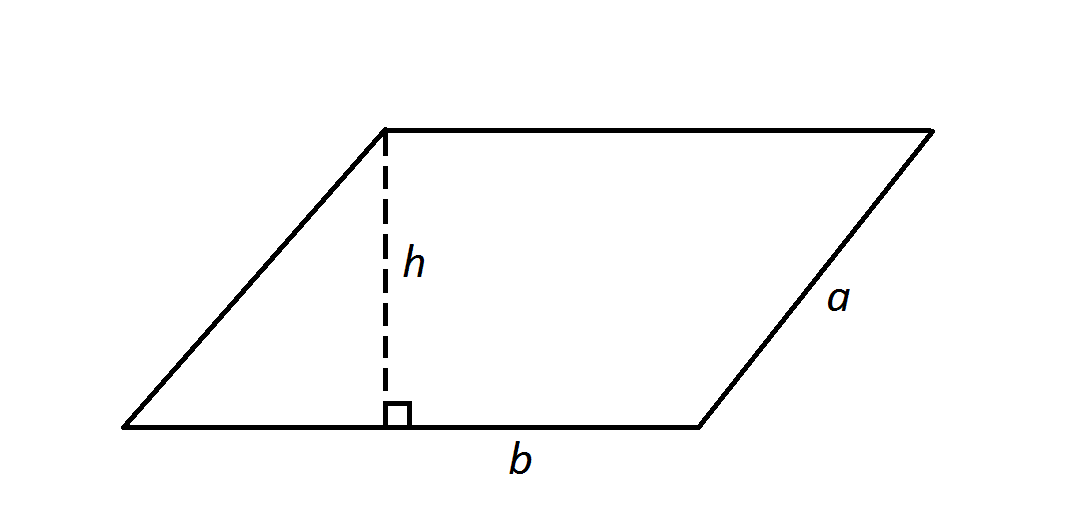
Example Question #1 : How To Find The Area Of A Parallelogram

Parallelogram

Note: Figure NOT drawn to scale

In the above diagram, $a = 14\; \textrm{in} ,b=16\; \textrm{in},h=10\; \textrm{in}$

Give the area of the parallelogram.

Possible Answers:

$120\; \textrm{in}^{2}$

$160\; \textrm{in}^{2}$

$140\; \textrm{in}^{2}$

$80\; \textrm{in}^{2}$

$224\; \textrm{in}^{2}$

Correct answer:

$160\; \textrm{in}^{2}$

Explanation:

The area of a parallelogram is its base multiplied by its height - represented by and here:

$A = bh = 16 \cdot 10 = 160$

Note that the value of is irrelevant.

Report an Error

Example Question #2 : Parallelograms

A given parallelogram has a base $20\:cm$ in length, a height $16\:cm$ in length, and a side of length $18\:cm$ opposite the height. What is the area of the parallelogram?

Possible Answers:

$36\:cm^{2}$

$38\:cm^{2}$

$320\:cm^{2}$

$288\:cm^{2}$

$360\:cm^{2}$

Correct answer:

$320\:cm^{2}$

Explanation:

The formula for the area of a parallelogram is $A=b\times h$ , with base and height represented by and , respectively. Substituting values from the question:

$A=20\:cm\times 16\:cm$

$A=320\:cm^{2}$

Report an Error

Example Question #2 : How To Find The Area Of A Parallelogram

A parallelogram has a height of $10\:cm$ in length, a side of length $12\:cm$ opposite the height, and a base of $24\:cm$ . What is the area of the parallelogram?

Possible Answers:

$260\:cm^{2}$

$120\:cm^{2}$

$140\:cm^{2}$

$240\:cm^{2}$

$288\:cm^{2}$

Correct answer:

$240\:cm^{2}$

Explanation:

Given base (b) and height (h) , $A=b\times h$ .

Substituting the values from our question:

$A=24\:cm\times 10\:cm$

$A=240\:cm^{2}$

Report an Error

Example Question #3 : Parallelograms

A parallelogram has a base of length $30\:cm$ , a height of length $15\:cm$ , and a side of length $13\:cm$ . What is the area of the parallelogram?

Possible Answers:

$390\:cm^{2}$

$450\:cm^{2}$

$195\:cm^{2}$

$45\:cm^{2}$

$300\:cm^{2}$

Correct answer:

$450\:cm^{2}$

Explanation:

Given base (b) and height (h) , $A=b\times h$ .

Substituting the values from our question:

$A= 30\:cm\times15\:cm$

$A=450\:cm^{2}$

Report an Error

Example Question #4 : Parallelograms

Find the area of a parallelogram with a height of $9\:cm$ , a base of $8\:cm$ , and a side length of $7\:cm$ .

Possible Answers:

$63\:cm^{2}$

$72\:cm$

$63\:cm$

$72\:cm^{2}$

$56\:cm^{2}$

Correct answer:

$72\:cm^{2}$

Explanation:

The area of a parallelogram with height and base can be found with the equation A=bh . Consequently:

A=bh

$A=(9\:cm)(8\:cm)$

$A=72\:cm^{2}$

Report an Error

Example Question #3 : How To Find The Area Of A Parallelogram

Find the area of a parallelogram with a height of $12\:cm$ , base of $11\:cm$ , and a side length of $7\:cm$ .

Possible Answers:

$132\:cm^{2}$

$77\:cm$

$132\:cm$

$84\:cm^{2}$

$77\:cm^{2}$

Correct answer:

$132\:cm^{2}$

Explanation:

The area of a parallelogram with height and base can be found with the equation A=bh . Consequently:

A=bh

$A=(12\:cm)(11\:cm)$

$A=132\:cm^{2}$

Report an Error

Example Question #2 : How To Find The Area Of A Parallelogram

Find the area of the following parallelogram:

Note: The formula for the area of a parallelogram is $A=b\times h$ .

Possible Answers:

$30\: in^2$

$50\: in^2$

$60\: in^2$

$32\: in^2$

Correct answer:

$50\: in^2$

Explanation:

The base of the parallelogram is 10, while the height is 5.

$A=b\times h$

$A=10\times5=50\: in^2$

Report an Error

Example Question #4 : Geometry

Find the area:

Question_5

Possible Answers:

$\small 24$

$\small 16$

$\small 32$

$\small 12$

Correct answer:

$\small 24$

Explanation:

The area of a parallelogram can be determined using the following equation:

$\small A=bh$

Therefore,

$\small A=8\times3=24$

Report an Error

Example Question #6 : Parallelograms

Parallelogram

Find the area of the given parallelogram if h=5, b=8, c=6 .

Possible Answers:

Correct answer:

Explanation:

In order to find the area of a parallelogram, we need to find the product of the base length and height.

A=(b)(h)=(8)(5)=40

Notice that only two of the given values were needed to slove this problem.

Report an Error

View SSAT- Middle Level Tutors

Omar
Certified Tutor

Arizona State University, Bachelors, Civil Engineering.

View SSAT- Middle Level Tutors

Carneta
Certified Tutor

Langston University, Bachelor in Arts, Theater Arts.

View SSAT- Middle Level Tutors

Ingrid
Certified Tutor

Northern Illinois University, Bachelor of Science, Elementary Education. Northern Illinois University, Master of Science, Cur...

All SSAT Middle Level Math Resources

10 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SSAT Tutors in Phoenix, Algebra Tutors in Denver, Biology Tutors in San Diego, Calculus Tutors in Washington DC, Calculus Tutors in New York City, Math Tutors in Los Angeles, Spanish Tutors in Washington DC, GRE Tutors in Los Angeles, French Tutors in Philadelphia, Reading Tutors in Miami

Popular Courses & Classes

Spanish Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Houston, ACT Courses & Classes in Miami, SSAT Courses & Classes in Los Angeles, Spanish Courses & Classes in Chicago, SAT Courses & Classes in Denver, SAT Courses & Classes in San Francisco-Bay Area, MCAT Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in New York City, LSAT Courses & Classes in Phoenix

Popular Test Prep

LSAT Test Prep in Houston, SAT Test Prep in Los Angeles, ISEE Test Prep in San Diego, SSAT Test Prep in New York City, ISEE Test Prep in New York City, SAT Test Prep in San Diego, ACT Test Prep in Dallas Fort Worth, ISEE Test Prep in Chicago, MCAT Test Prep in Washington DC, MCAT Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Middle Level Math : How to find the area of a parallelogram

Study concepts, example questions & explanations for SSAT Middle Level Math

All SSAT Middle Level Math Resources

Example Questions

Example Question #1 : How To Find The Area Of A Parallelogram

Example Question #2 : Parallelograms

Example Question #2 : How To Find The Area Of A Parallelogram

Example Question #3 : Parallelograms

Example Question #4 : Parallelograms

Example Question #3 : How To Find The Area Of A Parallelogram

Example Question #2 : How To Find The Area Of A Parallelogram

Example Question #4 : Geometry

Example Question #6 : Parallelograms

All SSAT Middle Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: