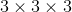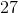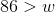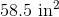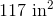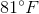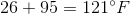In order to solve this problem we need to create a ratio with the given information. It says that for every  vote cast for candidate A, candidate B got  votes. We can write the following ratio.

Now substitute in the given numbers.

We know that candidate B received  votes. Write a new ratio.

Now, use the original relationship to create a proportion and solve for the number of votes that candidate A received.

Cross multiply and solve for .

Simplify.

Divide both sides of the equation by .

Solve.

When expanding an exponent, we multiply the base by itself for the number indicated by the exponential value.

In this case, our base number is  and our exponential value is . So we multiply  by itself  times. 

Remember, the question asks us for the multiplication problem, not the answer to . Because of this,  is our correct answer.

To solve this problem we need to use the distributive property. This property is used to multiply a term outside of a set of parentheses by each of the terms in the parentheses. 

Now we have 

This expression is simplified because we cannot add  to  because  has a variable  attached to it. 

Our number sentence has the phrase "less than" which means we have an inequality. 

" is less than " can be written as  because we replace the words "less than " with the less than symbol. 

In order to solve this problem, we need to recall the formula for area of a right triangle: 

 or 

Now we can substitute in our side lengths from the question:.

The formula used to find volume of a rectangular prism is as follows:

Substitute our side lengths:

Remember, volume is always written with cubic units because volume is how many cubic units can fit inside of a figure. 

In order to solve this question, we need to first recall how to find the area of a rectangle.

Substitute in the given values in the equation and solve for .

Divide both sides by 

Dividing by a fraction is the same as multiplying by its inverse or reciprocal.

Find the reciprocal of 

Simplify and rewrite.

Multiply and solve.

Reduce.

The width of the fracking site is 

There are several ways that we could solve this problem. First, we can say that the temperature in New Castle is  below zero and in Tucson it is  above zero; therefore we can say:

Also, we can solve this problem by using a number line. New Castle’s temperature is  units away from zero and Tucson’s is  units away.  

We can see that Tucson is  warmer than New Castle.

The dot plot is on a number line that is numbered from .  is the highest number on the number line, but there are no dots above that number, which means no one found  pencils in their desk.  is the next highest number, and there are two dots over the number on the number line; thus, the correct answer is 

To answer this question, we can look at our graph and see how far each bar in the histogram raises:

We are looking for the shortest bar because we want to know during which month the least amount of flowers were sold. We can see that in March only  flowers were sold, which is the least for the period that was observed.