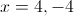We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Algebra II : Solving and Graphing Exponential Equations

Study concepts, example questions & explanations for Algebra II

Create An Account

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #331 : Sat Subject Test In Math I

What is the horizontal asymptote of the graph of the equation $y = -2e^{x-3} -5$ ?

Possible Answers:

y=-5

$y=-\frac{5}{2}$

y=-2

y=3

y=5

Correct answer:

y=-5

Explanation:

The asymptote of this equation can be found by observing that $e^{x-3} > 0$ regardless of . We are thus solving for the value of as $e^{x-3}$ approaches zero.

$-2e^{x-3} < -2\cdot 0$

$-2e^{x-3} < 0$

$-2e^{x-3} -5 < 0-5$

$-2e^{x-3} -5 < -5$

y<-5

So the value that cannot exceed is , and the line y = -5 is the asymptote.

Report an Error

Example Question #1 : Solving Exponential Functions

What is/are the asymptote(s) of the graph of the function

$f(x) = 5e^{x-2}-2$ ?

Possible Answers:

x=2

y = -2

y = -2, x=-2

y = -2, x=2

x=-2

Correct answer:

y = -2

Explanation:

An exponential equation of the form $f(x) = ae^{x-h} +k$ has only one asymptote - a horizontal one at y = k . In the given function, k = -2 , so its one and only asymptote is y = -2 .

Report an Error

Example Question #2 : Find The Equations Of Vertical Asymptotes Of Tangent, Cosecant, Secant, And Cotangent Functions

Find the vertical asymptote of the equation.

$y=\frac{x^2-9}{x^2-16}$

Possible Answers:

There are no vertical asymptotes.

x=4, -4

x=1

x=0

x=4

Correct answer:

x=4, -4

Explanation:

To find the vertical asymptotes, we set the denominator of the function equal to zero and solve.

0=x^2-16

16=x^2

$\sqrt{16}=\sqrt{x^2}$

4, -4=x

Report an Error

Example Question #1 : Asymptotes

Determine the asymptotes, if any: $y=\frac{x^2-2x+1}{x^2-1}$

Possible Answers:

x=-1

$x=-\frac{1}{2}$

$x=\pm1$

x=1

$\textup{There are no asymptotes.}$

Correct answer:

x=-1

Explanation:

Factorize both the numerator and denominator.

$y=\frac{x^2-2x+1}{x^2-1}=\frac{(x-1)(x-1)}{(x+1)(x-1)}$

Notice that one of the binomials will cancel.

The domain of this equation cannot include $x=\pm1$ .

The simplified equation is:

$y=\frac{x-1}{x+1}$

Since the (x-1) term canceled, the (x-1) term will have a hole instead of an asymptote.

Set the denominator equal to zero.

x+1=0

Subtract one from both sides.

x=-1

There will be an asymptote at only: x=-1

The answer is: x=-1

Report an Error

Example Question #1 : Find The Equations Of Vertical Asymptotes Of Tangent, Cosecant, Secant, And Cotangent Functions

Which of the choices represents asymptote(s), if any? $y=\frac{2x^2+2x}{x^2-8x-9}$

Possible Answers:

$x=1, 9\textup{ and } y= -\frac{2}{5}$

x=1, 9

$\textup{There are no asymptotes.}$

x=9

$x=9\textup{ and }y=\frac{2}{5}$

Correct answer:

x=9

Explanation:

Factor the numerator and denominator.

$y=\frac{2x^2+2x}{x^2-8x-9} = \frac{2x(x+1)}{(x-9)(x+1)}$

Notice that the (x+1) terms will cancel. The hole will be located at x=-1 because this is a removable discontinuity.

$y=\frac{2x}{x-9}$

The denominator cannot be equal to zero. Set the denominator to find the location where the x-variable cannot exist.

$x-9\neq0$

$x\neq9$

The asymptote is located at x=9 .

Report an Error

Example Question #1 : Asymptotes

Where is an asymptote located, if any? $y=\frac{2x-4}{x^2-4}$

Possible Answers:

x=2

$\textup{There is no asymptote.}$

x=-2

y=2

y=-2

Correct answer:

x=-2

Explanation:

Factor the numerator and denominator.

2x-4 = 2(x-2)

x^2-4 = (x+2)(x-2)

Rewrite the equation.

$y=\frac{2x-4}{x^2-4}=\frac{ 2(x-2)}{(x+2)(x-2)}=\frac{2}{x+2}$

Notice that the (x-2) will cancel. This means that the root of (x-2) will be a hole instead of an asymptote.

Set the denominator equal to zero and solve for x.

x+2=0

x=-2

An asymptote is located at: x=-2

The answer is: x=-2

Report an Error

Example Question #1 : Asymptotes

Consider the exponential function y=2^x+3 . Determine if there are any asymptotes and where they lie on the graph.

Possible Answers:

There are no asymptotes. goes to positive infinity in both the and directions.

There is one vertical asymptote at y=2 .

There is one horizontal asymptote at y=3 .

There is one vertical asymptote at y=3 .

Correct answer:

There is one horizontal asymptote at y=3 .

Explanation:

For positive values, increases exponentially in the direction and goes to positive infinity, so there is no asymptote on the positive -axis. For negative values, as decreases, the term 2^x becomes closer and closer to zero so approaches as we move along the negative axis. As the graph below shows, this is forms a horizontal asymptote.

Exp_asymp

Report an Error

Example Question #1 : Solving Exponential Equations

Solve the equation for .

$\small 9^x=3^6$

Possible Answers:

$\small x=2$

$\small x=1$

$\small x=3$

$\small x=0$

Correct answer:

$\small x=3$

Explanation:

Begin by recognizing that both sides of the equation have a root term of .

$\small 9^x=3^6$

(3^2)^x=3^6

Using the power rule, we can set the exponents equal to each other.

$3^{(2*x)}=3^6$

$\small 2x=6$

$\small x=3$

Report an Error

Example Question #1 : Solving And Graphing Exponential Equations

Solve the equation for .

$\small 3^{2x}=81$

Possible Answers:

x=1

x=9

x=2

x=3

x=4

Correct answer:

x=2

Explanation:

Begin by recognizing that both sides of the equation have the same root term, .

$\small 3^{2x}=81$

$\small 3^{2x}=9^2$

$3^{2x}=(3^2)^2$

We can use the power rule to combine exponents.

$3^{2x}=3^4$

Set the exponents equal to each other.

2x=4

$\small x=2$

Report an Error

Example Question #1 : Solving Exponential Equations

In 2009, the population of fish in a pond was 1,034. In 2013, it was 1,711.

Write an exponential growth function of the form $y=ab^{x}}$ that could be used to model , the population of fish, in terms of , the number of years since 2009.

Possible Answers:

y=1034(1.1342)^x

y=1.35(1.0011)^x

y=1.2(1711)^x

y=1711(1.3932)^x

y=1.1(1034)^x

Correct answer:

y=1034(1.1342)^x

Explanation:

Solve for the values of a and b:

In 2009, y=1034 and x=0 (zero years since 2009). Plug this into the exponential equation form:

$1034=ab^{(0)}$ . Solve for to get .

In 2013, y=1711 and x=4 . Therefore,

1711=ab^4 or 1711=(1034)b^4 . Solve for to get

$b=\sqrt[4]{\frac{1711}{1034}}\approx1.1342$ .

Then the exponential growth function is

$y=1034(1.1342)^{x}$ .

Report an Error

View Algebra 2 Tutors

Blossom
Certified Tutor

University of Maryland-Baltimore County, Bachelor of Science, Computer Science.

View Algebra 2 Tutors

Dalton
Certified Tutor

University of Massachusetts Amherst, Doctor of Philosophy, Mathematics.

View Algebra 2 Tutors

Justin
Certified Tutor

Vanderbilt University, Bachelor, Computer Science, Mathematics, & Philosophy.

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Reading Tutors in New York City, LSAT Tutors in Houston, Statistics Tutors in Seattle, Physics Tutors in San Diego, Physics Tutors in Phoenix, GRE Tutors in Houston, Statistics Tutors in Chicago, Algebra Tutors in Houston, Chemistry Tutors in Denver, Spanish Tutors in Boston

Popular Courses & Classes

SAT Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in Washington DC, SAT Courses & Classes in Phoenix, GRE Courses & Classes in San Diego, GRE Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Atlanta, Spanish Courses & Classes in New York City, SAT Courses & Classes in Houston, ACT Courses & Classes in Philadelphia, GRE Courses & Classes in Seattle

Popular Test Prep

SAT Test Prep in Washington DC, MCAT Test Prep in Houston, MCAT Test Prep in Denver, ISEE Test Prep in Washington DC, GRE Test Prep in San Diego, GRE Test Prep in Seattle, ISEE Test Prep in Atlanta, ACT Test Prep in Los Angeles, MCAT Test Prep in Seattle, SSAT Test Prep in Boston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra II : Solving and Graphing Exponential Equations

Study concepts, example questions & explanations for Algebra II

All Algebra II Resources

Example Questions

Example Question #331 : Sat Subject Test In Math I

Example Question #1 : Solving Exponential Functions

Example Question #2 : Find The Equations Of Vertical Asymptotes Of Tangent, Cosecant, Secant, And Cotangent Functions

Example Question #1 : Asymptotes

Example Question #1 : Find The Equations Of Vertical Asymptotes Of Tangent, Cosecant, Secant, And Cotangent Functions

Example Question #1 : Asymptotes

Example Question #1 : Asymptotes

Example Question #1 : Solving Exponential Equations

Example Question #1 : Solving And Graphing Exponential Equations

Example Question #1 : Solving Exponential Equations

All Algebra II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: