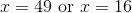We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Algebra II : Solving Radical Equations

Study concepts, example questions & explanations for Algebra II

Create An Account

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Solving And Graphing Radicals

Solve for :

$x + 3 \sqrt{x} = 28$

Possible Answers:

$x = -49 \textup{ or }x = 16$

$x = i \sqrt{7} \textup{ or }x = 2$

None of the other responses is correct.

$x = 49 \textup{ or }x = 16$

$x = - \sqrt{7} \textup{ or }x = 2$

Correct answer:

None of the other responses is correct.

Explanation:

One way to solve this equation is to substitute for $\sqrt{x}$ and, subsequently, $u^{2}$ for :

$x + 3 \sqrt{x} = 28$

$u^{2} + 3 u = 28$

$u^{2} + 3 u - 28 = 0$

Solve the resulting quadratic equation by factoring the expression:

(u+7)(u-4) = 0

Set each linear binomial to sero and solve:

u + 7 = 0

u = -7

u - 4 = 0

u = 4

Substitute back:

u = -7

$\sqrt{x}= -7$ - this is not possible.

u = 4

$\sqrt{x}= 4$

x = 16 - this is the only solution.

None of the responses state that x = 16 is the only solution.

Report an Error

Example Question #1 : Solving Radical Equations

Solve the following radical equation.

$\frac{10\sqrt{8}}{\sqrt{16}} + 3\sqrt{2}$

Possible Answers:

$13\sqrt{2}$

$8\sqrt{2}$

$\frac{10}{\sqrt{2} } +3\sqrt{2}$

$5\sqrt{8} + 3\sqrt{2}$

Correct answer:

$8\sqrt{2}$

Explanation:

We can simplify the fraction:

$\frac{10\sqrt{8}}{\sqrt{16}} = \frac{10\sqrt{4\times 2}}{4}=\frac{10(2\sqrt{2})}{4} =\frac{20\sqrt{2}}{4}=5\sqrt{2}$

Plugging this into the equation leaves us with:

$5\sqrt{2} + 3\sqrt{2} = 8\sqrt{2}$

Note: Because they are like terms, we can add them.

Report an Error

Example Question #3 : Solving Radical Equations

Solve the following radical equation.

$\sqrt{x-6} =2$

Possible Answers:

$x=6 +\sqrt{2}$

x=2

x=-10

x=10

Correct answer:

x=10

Explanation:

In order to solve this equation, we need to know that

$(\sqrt{x-6})^{2} = x-6$

How? Because of these two facts:

$\sqrt{x-6} = (x-6)^{\frac{1}{2}}$
Power rule of exponents: when we raise a power to a power, we need to mulitply the exponents:

$\frac{1}{2} \times2=1$

With this in mind, we can solve the equation:

$\sqrt{x-6} =2$

In order to eliminate the radical, we have to square it. What we do on one side, we must do on the other.

$(\sqrt{x-6})^{2} = 2^{2}$

x-6=4

x=10

Report an Error

Example Question #4 : Solving Radical Equations

Solve the following radical equation.

$\sqrt{\frac{x}{2}}=5$

Possible Answers:

x=10

x=50

$x=2\sqrt{5}$

$x=\sqrt{10}$

Correct answer:

x=50

Explanation:

In order to solve this equation, we need to know that

$\bigg(\sqrt{\frac{x}{2}}\bigg)^{2} =\frac{x}{2}$

Note: This is due to the power rule of exponents.

With this in mind, we can solve the equation:

$\sqrt{\frac{x}{2}} =5$

In order to get rid of the radical we square it. Remember what we do on one side, we must do on the other.

$\bigg(\sqrt{\frac{x}{2}}\bigg)^{2} =5^{2}$

$\frac{x}{2} =25$

$\frac{2}{1} \bigg(\frac{x}{2}\bigg)=25\bigg(\frac{2}{1}\bigg)$

x=50

Report an Error

Example Question #5 : Solving Radical Equations

Solve for x: $\sqrt{2x+1} = 11$

Possible Answers:

$\frac{\sqrt{11} + 1 }{2}$

240

$\sqrt{5}$

Correct answer:

Explanation:

To solve, perform inverse opperations, keeping in mind order of opperations:

$\sqrt{2x+1} = 11$ first, square both sides

2x + 1 = 121 subtract 1

2x = 120 divide by 2

x = 60

Report an Error

Example Question #4 : Solving Radical Equations

Solve for x: $(\sqrt{x} + 19 )^2 = 10,000$

Possible Answers:

507.3158

1,899.5

9,999.999

6,561

Correct answer:

6,561

Explanation:

To solve, perform inverse opperations, keeping in mind order of opperations:

$(\sqrt x + 19 ) ^ 2 = 10,000$ take the square root of both sides

$\sqrt x + 19 = 100$ subtract 19 from both sides

$\sqrt{x } = 81$ square both sides

x = 6,561

Report an Error

Example Question #1 : Solving And Graphing Radicals

Solve for x: $5\sqrt{x - 12 } = 20$

Possible Answers:

40.96

Correct answer:

Explanation:

To solve, use inverse opperations keeping in mind order of opperations:

$5\sqrt {x-12} = 20$ divide both sides by 5

$\sqrt{x-12 } = 4$ square both sides

x - 12 = 16 add 12 to both sides

x = 28

Report an Error

Example Question #1 : Solving Radical Equations

Solve for .

$\sqrt{x}=4$

Possible Answers:

$\pm2$

Correct answer:

Explanation:

$\sqrt{x}=4$ To get rid of the radical, we square both sides.

x=4^2=16

Report an Error

Example Question #2 : Solving Radical Equations

Solve for .

$\sqrt{x}=-5$

Possible Answers:

$\pm5$

$\pm25$

No answer

Correct answer:

No answer

Explanation:

To get rid of the radical, we need to square both sides. The issue is radicals don't generate negative numbers unless we talk about imaginary numbers. In this case, our answer choice should be no answer.

Report an Error

Example Question #323 : Radicals

Solve for .

$\sqrt{x+1}=5$

Possible Answers:

Correct answer:

Explanation:

$\sqrt{x+1}=5$ Square both sides to get rid of the radical.

x+1=5^2=25 Subtract on both sides.

x=24

Report an Error

View Algebra 2 Tutors

Anne
Certified Tutor

University of Maryland-Baltimore, Doctor of Science, Accounting.

View Algebra 2 Tutors

Isabella
Certified Tutor

Iowa State University, Bachelor of Science, Mathematics.

View Algebra 2 Tutors

Margaret
Certified Tutor

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Algebra Tutors in Chicago, Math Tutors in Houston, Reading Tutors in Atlanta, Biology Tutors in San Francisco-Bay Area, Calculus Tutors in San Diego, ISEE Tutors in Dallas Fort Worth, Math Tutors in New York City, Biology Tutors in Los Angeles, Biology Tutors in Washington DC, English Tutors in New York City

Popular Courses & Classes

GMAT Courses & Classes in Atlanta, GRE Courses & Classes in Los Angeles, ISEE Courses & Classes in Houston, SSAT Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in Los Angeles, ISEE Courses & Classes in Miami, GMAT Courses & Classes in New York City, ISEE Courses & Classes in Philadelphia, GMAT Courses & Classes in Denver, SAT Courses & Classes in Boston

Popular Test Prep

MCAT Test Prep in Atlanta, GRE Test Prep in Atlanta, GRE Test Prep in Dallas Fort Worth, GRE Test Prep in Houston, GRE Test Prep in New York City, SAT Test Prep in Los Angeles, LSAT Test Prep in Atlanta, MCAT Test Prep in Miami, ISEE Test Prep in New York City, GRE Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra II : Solving Radical Equations

Study concepts, example questions & explanations for Algebra II

All Algebra II Resources

Example Questions

Example Question #1 : Solving And Graphing Radicals

Example Question #1 : Solving Radical Equations

Example Question #3 : Solving Radical Equations

Example Question #4 : Solving Radical Equations

Example Question #5 : Solving Radical Equations

Example Question #4 : Solving Radical Equations

Example Question #1 : Solving And Graphing Radicals

Example Question #1 : Solving Radical Equations

Example Question #2 : Solving Radical Equations

Example Question #323 : Radicals

All Algebra II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: