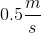The velocity of the water can be determined from the following formula:

\(\displaystyle v = \frac{\dot{V}}{A}\)

We need to calculate the volumetric flow rate and the cross-sectional area. For the flow rate:

\(\displaystyle \dot m = \dot V \cdot \rho_{water}\)

Rearrange to solve for volumetric flow rate:

\(\displaystyle \dot V = \frac{\dot m}{\rho_{water}} = \frac{800\frac{kg}{s}}{1000\frac{kg}{m^3}} = 0.8 \frac{m^3}{s}\)

Next, calculate cross-sectional area:

\(\displaystyle A = \pi \frac{d^2}{4} = \pi \frac{(2m)^2}{4} = \pi m^2\)

Now we can solve for the velocity:

\(\displaystyle v = \frac{0.8\frac{m^3}{s}}{\pi m^2} = 0.25 \frac{m}{s}\)

To find the answer to this question, we'll need to use the continuity equation to determine the flow rate, which will be the same in both pipes.

\(\displaystyle vA=f\)

\(\displaystyle v_{1}A_{1}=v_{2}A_{2}\)

We'll also need to calculate the area of the pipe using the equation:

\(\displaystyle A=\pi r^{2}\)

\(\displaystyle A_{1}=\pi r_{1}^{2}=\pi (0.5\m)^{2}=0.25\pi m^{2}\)

\(\displaystyle A_{2}=\pi r_{2}^{2}=\pi \left ( 0.25 m\right )^{2}=0.0625\pi m^{2}\)

Solve the combined equation for \(\displaystyle v_2\) and plug in known values to find the velocity of the water through the second pipe.

\(\displaystyle v_{2}=\frac{v_{1}A_{1}}{A_{2}}\)

\(\displaystyle v_{2}=\frac{(5 \frac{m}{s})(0.25\pi m^{2})}{0.0625\pi m^{2}}=20 \frac{m}{s}\)

Use the continuity equation for incompressible fluids. 

\(\displaystyle A_1v_1 =A_2v_2\)

The cross sectional area of the garden hose at both ends are circular regions. Rewrite the equation replacing areas with the formula for an area of a circle and solve for the velocity at the second point.

\(\displaystyle \left(\frac{\pi d_1^2}{4}\right)v_1 =\left(\frac{\pi d_2^2}{4}\right)v_2\)

\(\displaystyle v_2 = \frac{v_1 d_1^2}{d_2^2}= \frac{1\frac{{m}}{{s}}(3^2)}{2^2}= \left(\frac{3}{2}\right)^2=2.25 \frac{{m}}{{s}}\)

This is a volume flow rate problem. Because the water is an incompressible fluid, we can apply the flow rate equation:

\(\displaystyle A_{1}* v_{1}=A_{2}* v_{2}\)

Find the surface area of the pond:

\(\displaystyle A_{1}=\pi r^2 = 3.14* 200^2 =1.3* 10^5m^2\)

Substitute into the flow rate equation:

\(\displaystyle 1.3*10^5 * 2.1*10^{-5}=0.5* v_2\)

\(\displaystyle v_2=5.56\frac{m}{s}\)

When the area halves, the velocity of the fluid will double. However, the volume flow rate (the product of these two quantities) will remain the same. In other words, the volume of water flowing through location 1 per second is the same as the volume of water flowing through location 2 per second. 

The volumetric flow rate of fluid is found using the equation:

\(\displaystyle Q=v*a\)

Where \(\displaystyle v\) is the velocity of the fluid and \(\displaystyle a\) is the cross-sectional area of the space through which the fluid is flowing.

In this problem the cross-section of the pipe is a circle. The area of the cross-section is:

\(\displaystyle a=\pi*r^{2}=\pi*\left ( \frac{12}{2} \right )^{2}\approx113.04m^2\)

The volumetric flow rate is:

\(\displaystyle Q=v*a=5*113.04=565.2\frac{m^3}{s}\)

The volumetric flow rate of fluid is found using the equation:

\(\displaystyle Q=v*a\)

Where \(\displaystyle v\) is the velocity of the fluid and \(\displaystyle a\) is the cross-sectional area of the space through which the fluid is flowing.

In this problem the cross-section of the pipe is a square. The area of the cross-section is:

\(\displaystyle a=4*4=16m^2\)

The volumetric flow rate is:

\(\displaystyle Q=v*a=7*16=112\frac{m^3}{s}\)

The volumetric flow rate of fluid is found using the equation:

\(\displaystyle Q=v*a\)

Where \(\displaystyle v\) is the velocity of the fluid and \(\displaystyle a\) is the cross-sectional area of the space through which the fluid is flowing. Use the continuity equation, we see that \(\displaystyle Q_{in}=Q_{out}\), therefore

\(\displaystyle v_{in}*a_{in}=v_{out}*a_{out}\)

In this problem, the cross-section of the pipe is a circle, which is

\(\displaystyle a_{in}=\pi*r^{2}=\pi*\left ( \frac{30}{2} \right )^{2}\approx706.5m^2\)

The area of the exit cross-section is:

\(\displaystyle a_{out}=\pi*r^{2}=\pi*\left ( \frac{15}{2} \right )^{2}\approx176.71m^2\)

Plug in these variables into the continuity equation and solve:

\(\displaystyle 15*706.5=v_{out}*176.71\)

\(\displaystyle v_{out}=59.97\frac{m}{s}\)

The volumetric flow rate of fluid is found using the equation:

\(\displaystyle Q=v*a\)

Where \(\displaystyle v\) is the velocity of the fluid and \(\displaystyle a\) is the cross-sectional area of the space through which the fluid is flowing.

Use the continuity equation, we see that \(\displaystyle Q_{in}=Q_{out}\), therefore:

\(\displaystyle v_{in}*a_{in}=v_{out}*a_{out}\)

In this problem,

The cross-section of the pipe is a circle, which is:

\(\displaystyle a_{in}=\pi*r^{2}=\pi*\left ( \frac{26}{2} \right )^{2}\approx530.93m^2\)

Plugging our variables into the continuity equation gives us

\(\displaystyle 24*530.93=48*a_{out}\)

 \(\displaystyle a_{out}=265.46m^2\)

\(\displaystyle r_{out}=\sqrt{\frac{a}{\pi}}=\sqrt{\frac{265.46}{\pi}}=9.19m\)

\(\displaystyle d_{out}=2*r_{out}=2*9.19=18.38m\)

Based on the continuity equation, both parts of the flow must have the same volumetric flow rate.