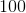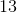Basic Arithmetic : Whole Numbers
Study concepts, example questions & explanations for Basic Arithmetic
All Basic Arithmetic Resources
Example Questions
Example Question #1 : Operations With Whole Numbers
Round to the nearest hundredth:
The hundredth place is the 2nd number after the decimal. Because the thousandth place is great than 5, we will need to round up to
Example Question #2 : Operations With Whole Numbers
Baseballs can only be bought in packages of 
1. Round 145 to the nearest 10:
Since there is a 5 in the ones place, 145 rounds up to 150.
2. Divide the rounded number of baseballs by 10 since they come in packages of 10:
150/10=15 packages
Example Question #2 : Operations With Whole Numbers
Round 
To round to the nearest ten, you need to take a look at the ones' place. Since the ones' place is greater than 
So then 
Example Question #3 : Operations With Whole Numbers
Round 
To figure out how to round the ones' place, we need to first look at the digit that's to the right of it. If the digit to the right of the ones' place is less than 5, then we leave the ones' place alone.
Since the tenths place is 1, we will leave the ones place alone.
Example Question #4 : Operations With Whole Numbers
Round 
To figure out how to round any number, look at the digit to the right of the place you're supposed to be rounding.
Since we want to round the hundreds place, look to the tens place first. If the tens place is greater than 5, then we round up. If the tens place is less than five, then leave the hundreds place alone.
Because the tens place is 7, we will need to round to 900.
Example Question #4 : Whole Numbers
What is 
An important thing to remember when rounding is knowing which place you're rounding to. In this problem, we our rounding to the ten-thousands place, therefore we need to take a look at two things: 1) which number appears in that place, and 2) what number appears immediately after it:
With this number, an 
Example Question #5 : Operations With Whole Numbers
If I had 
1. Add the ones places:
2. Add the tens places:
***don't forget to put the 3 down and carry the one to the hundreds place***
3. Add the hundreds place:
This makes your total:
Example Question #2 : Addition With Whole Numbers
Find the sum.
First add the digits in the ones colume, this would be 
Then add the digits in the tens colume, this would be 
Lastly, add the digits in the hundrends colume, this would be
Therefore the result is as follows:
Example Question #6 : Operations With Whole Numbers
What is the solution of the above operation?
We can see this because if we had 5 (represented by 
We have 7 objects total!
Example Question #7 : Operations With Whole Numbers
What is the solution of the above equation?
If x represents objects.
For 5:
For 6:
We can see that 11 objects result.
All Basic Arithmetic Resources
