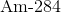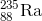By definition, isotopes of a given element have the same number of protons and electrons, but differ in the number of neutrons. This causes a difference in the mass number (protons + neutrons) as well. Neither the number of protons nor the number of electrons changes with different isotopes of the same element.

Isotopes are versions of an element with different numbers of neutrons. Hydrogen has three naturally occurring isotopes. $\displaystyle _{1}^{1}H$, sometimes called protium, contains one electron, one proton, and no neutrons. $\displaystyle ^{_{1}^{2}}H$, called deuterium, contains one electron, one proton, and one neutron. $\displaystyle _{1}^{3}H$, called tritium, contains one electron, one proton, and two neutrons. Hydrogen has no such isotope that contains three neutrons.

In order to find the molar mass of an atom from its isotopes and their natural abundances, use the following equation:

$\displaystyle \text{Atomic Mass}=\Sigma (\text{fraction of isotope})(\text{mass of isotope})$ for all the given isotopes.

Since chromium has four isotopes, we will write the following equation to find its atomic mass:

$\displaystyle \text{Atomic Mass of Chromium}=(0.0435\times 49.95)+(0.8379 \times 51.94)+(0.095\times 52.94)+(0.0236\times 53.94)=51.996amu$

Each element is defined by the number of protons its atoms contain. For example, hydrogen has one proton, helium has two protons, and lithium has three protons. Each element also has a characteristic number of neutrons. For example, hydrogen has zero neutrons, helium has two neutrons, and lithium has four neutrons.

Some elements, however, also have different "versions" of themselves: atoms which have a different number of neutrons, called isotopes. For example, there are three isotopes of hydrogen. $\displaystyle _{1}^{1}H$ has one proton and zero neutrons. $\displaystyle _{1}^{2}H$ has one proton and one neutron. Lastly, $\displaystyle _{1}^{3}H$ has one proton and two neutrons. Carbon is another such element that has different isotopes. 

Recall that when a particle undergoes alpha decay, the particle is emitting an alpha particle, which is the same as $\displaystyle \text{He-4}$.

Now, write the following equation of the alpha decay:

$\displaystyle _{93}^{288}\textrm{Np}\rightarrow_{91}^{284}\textrm{Pa}+_{2}^{4}\textrm{He}$

Thus, $\displaystyle \text{Pa-284}$ is the daughter nucleus.

For this question, we're told that $\displaystyle 83\%$ of a radioactive compound decays in $\displaystyle 24$ days. We're asked to determine the half-life for this compound.

The first thing we need to do is write an expression for radioactive decay. Remembering that radioactive decay processes follow a first-order reaction rate, we can use the following expression.

$\displaystyle A_{t}=A_{0}e^{-kt}$

We can further rewrite this expression as follows.

$\displaystyle ln(\frac{A_{t}}{A_{0}})=-kt$

Also, recall that in the beginning we are starting with $\displaystyle 100\%$ of the compound. After $\displaystyle 83\%$ of it has decayed, we will be left with $\displaystyle 17\%$ of the compound at time $\displaystyle t$. Furthermore, in order to solve for the half life, we will first need to find the rate constant, $\displaystyle k$.

$\displaystyle ln(\frac{17}{100})=-k(24\: days)$

$\displaystyle k=-\frac{ln(\frac{17}{100})}{24\: days}=0.0738\:days^{-1}$

Now that we have the rate constant for the decay reaction, we're equipped with what we need in order to calculate the half-life.

To solve for the half-life, we can derive an expression using one already shown above.

$\displaystyle ln(\frac{A_{t}}{A_{0}})=-kt$

$\displaystyle ln(\frac{50}{100})=-kt_{\frac{1}{2}}$

$\displaystyle t_{\frac{1}{2}}=\frac{-ln(\frac{1}{2})}{k}=\frac{ln(2)}{k}$

Now, using the above expression, we can plug in the value for the rate constant that we calculated in order to solve for the half-life.

$\displaystyle t_{\frac{1}{2}}=\frac{ln(2)}{k}=\frac{0.693}{0.0738\: days^{-1}}=9.39\:days$

Recall that beta decay occurs when the nucleus of the parent atom emits an electron. We can then write the following equation to illustrate the beta decay of thorium.

$\displaystyle _{90}^{235}\textrm{Th}\rightarrow _{91}^{235}\textrm{Pa}+_{-1}^{0}\textrm{e}$

Make sure that the atomic numbers and masses add up to the same on both sides of the equation.

In order to solve this problem we first must setup an equation representing the decay of $\displaystyle 3 \alpha$ particles. We know that an $\displaystyle \alpha$ particle is equivalent to $\displaystyle _{2}^{4}\textrm{\textbf{He}}$, so we can write our radioactive decay equation as:

$\displaystyle _{84}^{214}\textrm{\textbf{Po}}\rightarrow 3*_{2}^{4}\textrm{\textbf{He}} +_{Y}^{V}\textrm{\textbf{X}}$

where $\displaystyle X$ is the unknown element

$\displaystyle Y$ is the atomic number

and $\displaystyle V$ is the mass number. We can create two equations. One to solve for the mass number and one to solve for the atomic number.

Let's start with the atomic number:

Since we have an atomic number of $\displaystyle 84$ on the reactants side of the equation we can set that equal to $\displaystyle 3*2$ (the combined atomic number of three $\displaystyle \alpha$ particles + $\displaystyle Y$.

As an equation this is written as:

$\displaystyle 84=6+y$

This simplifies to $\displaystyle y=78$. This means that is the atomic number, and we can identify the element by looking at the periodic table for element number $\displaystyle 78$ as the atomic number identifies the element. The element is Platinum also written as $\displaystyle Pt$.

Now we must solve for the mass number similarly:

Following the instructions above except for the mass number we create an equation with one unknown to solve for the mass number of $\displaystyle Pt$ produced by this decay.:

$\displaystyle 214=3*4+y$

therefore $\displaystyle y=202$

This means our final answer is $\displaystyle _{78}^{202}\textrm{\textbf{Pt}}$.

This can be double-checked by plugging the mass number and atomic number into the decay equation and simplifying it.

In order to determine the decay process that occurs we should check if the mass number charges or not in the decay. Since the mass number doesn't change we can eliminate any answer with  $\displaystyle \alpha$ decay in it.

Now we can write out our decay equation. Since the atomic numbers aren't written in the question we must find them on the periodic table, where elements are ordered by their atomic number. In the case of Thallium, we find that it is element number $\displaystyle 81$ and in the case of Polonium we find that it is element $\displaystyle 84$.

So our equation is as follows:

$\displaystyle _{81}^{204}\textrm{\textbf{Ti}}\rightarrow _{84}^{204}\textrm{\textbf{Po}}+ _{V}^{Y}\textrm{\textbf{X}}$

where $\displaystyle X$ is the element/particle name

$\displaystyle Y$ is the mass number

and $\displaystyle V$ is the atomic number.

Since the mass number is the same on both sides of the equation we know that it is equal to $\displaystyle 0$.

Now we see that the atomic number increases by $\displaystyle 3$, which is the equivalent of a $\displaystyle -3$ on the product side of the equation. The only particle in the answer choices that is capable of having a negative atomic number value is a $\displaystyle \beta$ particle, which is written as $\displaystyle _{-1}^{0}\textrm\textbf{\beta}$. In order to produce an atomic number change of $\displaystyle 3$ there must be $\displaystyle 3$ $\displaystyle \beta$ decays, which is the right answer.

Let's first look at the cases and determine which ones can maintain both the same atomic and mass number. We know that $\displaystyle \alpha$ decay produces a $\displaystyle _{2}^{4}\textrm{\textbf{He}}$ nucleus so this cannot be the right answer as both the mass number and atomic number change with $\displaystyle \alpha$ decay.

As for $\displaystyle \beta$ decay an electron is lost $\displaystyle _{-1}^{0}\textrm{\textbf{e}}$, so the atomic number increases, so therefore this cannot be the right answer.

In electron capture, an electron is gained so the atomic number decreases, so this cannot be the right answer either.

Positron emission means a positron $\displaystyle _{1}^{0}\textrm{\textbf{e+}}$ is lost, so this is not only equivalent to electron capture, but the atomic number changes by decreasing meaning this cannot be the right answer.

Therefore the right answer is gamma $\displaystyle \gamma$ decay, as in gamma decay the nuclei comes to a stable state and in order to do this must release ONLY energy, so neither the atomic number nor mass number change.