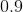All GRE Math Resources
Example Questions
Example Question #1 : Basic Squaring / Square Roots
Which quantity is greater? When
Quantity A

Quantity B
1
Quantity B is greater.
The relationship cannot be determined from the information given.
The two quantities are equal.
Quantity A is greater.
Quantity B is greater.
X must equal a number between 0 and 1.
If you square any decimal number in this range you will get an answer less than 1. Try 
Therefore Quantity B is always larger.
Example Question #372 : Arithmetic
Which is greater, when
Quantity A
Quantity B
Quantity A is greater
The relationship cannot be determined from the information given
The two quantities are equal
Quantity B is greater
The relationship cannot be determined from the information given
When 



When
But when
Therefore we cannot tell which is greater based on the information given.
Example Question #373 : Arithmetic
Which is greater, when
Quantity A
Quantity B
The relationship cannot be determined from the information given
Quantity B is greater
The two quantities are equal
Quantity A is greater
The relationship cannot be determined from the information given
When 



When
But when
Therefore we cannot tell which is greater based on the information given.
Example Question #372 : Arithmetic
Which is greater, when
Quantity A
Quantity B
Quantity B is greater
The two quantities are equal
Quantity A is greater
The relationship cannot be determined from the information given
Quantity A is greater
When 










Quantity A is greater.
Example Question #381 : Arithmetic
Which is greater, when
Quantity A
Quantity B
Quantity B is greater
The relationship cannot be determined from the information given
The two quantities are equal
Quantity A is greater
Quantity B is greater
When 




Quantity B is greater.
Example Question #2 : Basic Squaring / Square Roots
Find the square root of the following decimal:
The easiest way to find the square root of a fraction is to convert it into scientific notation.
The key is that the exponent in scientific notation has to be even for a square root because the square root of an exponent is diving it by two. The square root of 9 is 3, so the square root of 8.1 is a little bit less than 3, around 2.8
Example Question #3 : Basic Squaring / Square Roots
Find the square root of the following decimal:
To find the square root of this decimal we convert it into scientific notation.
Because 
Example Question #271 : Arithmetic
Find the square root of the following decimal:
This problem can be solve more easily by rewriting the decimal into scientific notation.
Because 
Example Question #272 : Arithmetic
Find the square root of the following decimal:
This problem becomes much simpler if we rewrite the decimal in scientific notation
Because 
Example Question #273 : Arithmetic
Find the square root of the following decimal:
To find the square root of this decimal we convert it into scientific notation.
Because 
All GRE Math Resources