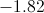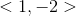Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Calculus II — Integrals

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Using Limits With Continuity

Function

The above graph depicts a function h(x) . Does $\lim_{x\rightarrow 1} h(x)$ exist, and why or why not?

Possible Answers:

$\lim_{x\rightarrow 1} h(x)$ does not exist because $f (1 ) \neq \lim_{x\rightarrow 1^{+}} h(x)$

$\lim_{x\rightarrow 1} h(x)$ exists because $\lim_{x\rightarrow 1^{-}} | h(x)| = \lim_{x\rightarrow 1^{+}} |h(x)|$

$\lim_{x\rightarrow 1} h(x)$ does not exist because $\lim_{x\rightarrow 1^{-}} h(x) \neq \lim_{x\rightarrow 1^{+}} h(x)$ .

$\lim_{x\rightarrow 1} h(x)$ exists because $f (1 ) = \frac{\lim_{x\rightarrow 1^{-}} h(x) + \lim_{x\rightarrow 1^{+ }} h(x)}{2}$

$\lim_{x\rightarrow 1} h(x)$ does not exist because $f (1 ) \neq \lim_{x\rightarrow 1^{-}} h(x)$

Correct answer:

$\lim_{x\rightarrow 1} h(x)$ does not exist because $\lim_{x\rightarrow 1^{-}} h(x) \neq \lim_{x\rightarrow 1^{+}} h(x)$ .

Explanation:

$\lim_{x\rightarrow 1} h(x)$ exists if and only if $\lim_{x\rightarrow 1^{-}} h(x) = \lim_{x\rightarrow 1^{+}} h(x)$ . As can be seen from the diagram, $\lim_{x\rightarrow 1^{-}} h(x) = 1$ , but $\lim_{x\rightarrow 1^{+}} h(x) = -1$ . Since $\lim_{x\rightarrow 1^{-}} h(x) \neq \lim_{x\rightarrow 1^{+}} h(x)$ , $\lim_{x\rightarrow 1} h(x)$ does not exist.

Report an Error

Example Question #2 : Using Limits With Continuity

Function

The above graph depicts a function f(x) . Does $\lim_{x\rightarrow 1} f(x)$ exist, and why or why not?

Possible Answers:

$\lim_{x\rightarrow 1} f(x)$ does not exist because $f(1) \neq \lim_{x\rightarrow 1^{-}} f(x)$

$\lim_{x\rightarrow 1} f(x)$ does not exist because is not continuaous at x = 1 .

$\lim_{x\rightarrow 1} f(x)$ exists because $\lim_{x\rightarrow 1^{+}} f(x) = \lim_{x\rightarrow 1^{-}} f(x)$

$\lim_{x\rightarrow 1} f(x)$ does not exist because $\lim_{x\rightarrow 1^{+}} f(x) \neq \lim_{x\rightarrow 1^{-}} f(x)$

$\lim_{x\rightarrow 1} f(x)$ does not exist because $f(1) \neq \lim_{x\rightarrow 1^{+}} f(x)$

Correct answer:

$\lim_{x\rightarrow 1} f(x)$ exists because $\lim_{x\rightarrow 1^{+}} f(x) = \lim_{x\rightarrow 1^{-}} f(x)$

Explanation:

$\lim_{x\rightarrow 1} f(x)$ exists if and only if $\lim_{x\rightarrow 1^{+}} f(x) = \lim_{x\rightarrow 1^{-}} f(x)$ ;

the actual value of f(1) is irrelevant, as is whether is continuous there.

As can be seen,

$\lim_{x\rightarrow 1^{+}} f(x) = 1$ and $\lim_{x\rightarrow 1^{-}} f(x) = 1$ ;

therefore, $\lim_{x\rightarrow 1^{+}} f(x) = \lim_{x\rightarrow 1^{-}} f(x)$ ,

and $\lim_{x\rightarrow 1} f(x)$ exists.

Report an Error

Example Question #3 : Calculus Ii — Integrals

A function is defined by the following piecewise equation:

$f(x)=\left\{\begin{matrix} x^{2}+4x-3, x<3\\10x-12, x\geq 3 \end{matrix}\right.$

At x=3 , the function is:

Possible Answers:

continuous

discontinuous

Correct answer:

continuous

Explanation:

The first step to determine continuity at a point is to determine if the function is defined at that point. When we substitute in 3 for , we get 18 as our -value. x=3 is thus defined for this function.

The next step is determine if the limit of the function is defined at that point. This means that the left-hand limit must be equal to the right-hand limit at x=3 . Substitution reveals the following:

$\lim_{x\rightarrow 3^{-}}f(x)=(3)^{2}+4(3)-3=9+12-3=18$

$\lim_{x\rightarrow 3^{+}}f(x)=10(3)-12=18$

Both sides of the function, therefore, approach a -value of 18.

Finally, we must ensure that the curve is smooth by checking the limit of the derivative of both sides.

$\lim_{x\rightarrow 3^{-}}f^{'}(x)=2(3)+4=10$

$\lim_{x\rightarrow 3^{+}}f^{'}(x)=10$

Since the function passes all three tests, it is continuous.

Report an Error

Example Question #1 : Limits

Function

The graph depicts a function g(x) . Does $\lim_{x\rightarrow 1} g(x)$ exist?

Possible Answers:

$\lim_{x\rightarrow 1} g(x)$ exists because g(x) is constant on $(-\infty , 1)$ .

$\lim_{x\rightarrow 1} g(x)$ does not exist because g(1) is undefined.

$\lim_{x\rightarrow 1} g(x)$ does not exist because is not continuous at x = 1 .

$\lim_{x\rightarrow 1} g(x)$ does not exist because $\lim_{x\rightarrow 1^{-}} g(x) \neq \lim_{x\rightarrow 1^{+}} g(x)$ .

$\lim_{x\rightarrow 1} g(x)$ exists because $\lim_{x\rightarrow 1^{-}} g(x) = \lim_{x\rightarrow 1^{+}} g(x)$ .

Correct answer:

$\lim_{x\rightarrow 1} g(x)$ exists because $\lim_{x\rightarrow 1^{-}} g(x) = \lim_{x\rightarrow 1^{+}} g(x)$ .

Explanation:

$\lim_{x\rightarrow 1}g(x)$ exists if and only if $\lim_{x\rightarrow 1^{+}} g(x) = \lim_{x\rightarrow 1^{-}} g(x)$ ; the actual value of f(1) is irrelevant.

As can be seen, $\lim_{x\rightarrow 1^{+}} g(x) = 1$ and $\lim_{x\rightarrow 1^{-}}g(x) = 1$ ; therefore, $\lim_{x\rightarrow 1^{+}} g(x) = \lim_{x\rightarrow 1^{-}} g(x)$ , and $\lim_{x\rightarrow 1} g(x)$ exists.

Report an Error

Example Question #1 : Understanding Polar Coordinates

The polar coordinates of a point are $\left(2.1, \frac{7\pi }{3}\right )$ . Give its -coordinate in the rectangular coordinate system (nearest hundredth).

Possible Answers:

-1.82

1.05

1.82

-1.05

4.20

Correct answer:

1.82

Explanation:

Given the polar coordinates $(r,\theta )$ , the -coordinate is $y= r \sin \theta$ . We can find this coordinate by substituting $r = 2.1, \theta = \frac{7\pi }{3}$ :

$y = r \sin \theta = 2.1 \cdot \sin \frac{7\pi }{3} \approx 2.1 \cdot 0.8660 \approx 1.82$

Report an Error

Example Question #2 : Understanding Polar Coordinates

The polar coordinates of a point are $\left(2.1, \frac{7\pi }{3}\right )$ . Give its -coordinate in the rectangular coordinate system (nearest hundredth).

Possible Answers:

1.05

-1.82

1.82

-1.05

4.20

Correct answer:

1.05

Explanation:

Given the polar coordinates $(r,\theta )$ , the -coordinate is $x= r \cos \theta$ . We can find this coordinate by substituting $r = 2.1, \theta = \frac{7\pi }{3}$ :

$x = r \cos \theta = 2.1 \cdot \cos \frac{7\pi }{3} = 2.1 \cdot 0.5 = 1.05$

Report an Error

Example Question #1 : Polar

The polar coordinates of a point are $\left(1.2, \frac{2\pi }{5}\right )$ . Give its -coordinate in the rectangular coordinate system (nearest hundredth).

Possible Answers:

1.26

3.88

0.37

1.14

3.69

Correct answer:

1.14

Explanation:

Given the polar coordinates $(r,\theta )$ , the -coordinate is $y= r \sin \theta$ . We can find this coordinate by substituting $r = 1.2, \theta = \frac{2\pi }{5}$ :

$y = r \cos \theta = 1.2 \cdot \sin \frac{2\pi }{5} \approx 1.2 \cdot 0.9511 \approx 1.14$

Report an Error

Example Question #1 : Calculus Ii — Integrals

The polar coordinates of a point are $\left(1.2, \frac{2\pi }{5}\right )$ . Give its -coordinate in the rectangular coordinate system (nearest hundredth).

Possible Answers:

3.88

1.14

1.26

3.69

0.37

Correct answer:

0.37

Explanation:

Given the polar coordinates $(r,\theta )$ , the -coordinate is $x= r \cos \theta$ . We can find this coordinate by substituting $r = 1.2, \theta = \frac{2\pi }{5}$ :

$x = r \cos \theta = 1.2 \cdot \cos \frac{2\pi }{5} \approx 1.2 \cdot 0.3090 \approx 0.37$

Report an Error

Example Question #5 : Parametric, Polar, And Vector

Find the vector where its initial point is (-1,4) and its terminal point is (2,2) .

Possible Answers:

<1,6>

<1,2>

<3,-2>

<1,-2>

Correct answer:

<3,-2>

Explanation:

We need to subtract the -coordinate and the -coordinates to solve for a vector when given its initial and terminal coordinates:

Initial pt: (-1,4)

Terminal pt: (2,2)

Vector: <2-(-1),2-4>

Vector:

Report an Error

Example Question #6 : Parametric, Polar, And Vector

Find the vector where its initial point is (-1,-5) and its terminal point is (2,3) .

Possible Answers:

$\left \langle1,8\right \rangle$

$\left \langle3,2\right \rangle$

$\left \langle3,8\right \rangle$

$\left \langle1,2\right \rangle$

Correct answer:

$\left \langle3,8\right \rangle$

Explanation:

We need to subtract the -coordinate and the -coordinate to solve for a vector when given its initial and terminal coordinates:

Initial pt: (-1,-5)

Terminal pt: (2,3)

Vector: $\left \langle 2-(-1),3-(-5)\right \rangle$

Vector: $\left \langle3,8\right \rangle$

Report an Error

View Tutors

Andrew
Certified Tutor

University of Wisconsin-Stevens Point, Bachelor of Science, Mathematics. University of Wisconsin-Oshkosh, Master of Science, ...

View Tutors

Linnea
Certified Tutor

Bethel University, Bachelor in Arts, Teaching English as a Second Language (ESL).

View Tutors

Magdy
Certified Tutor

Cairo University, Egypt, Bachelor of Science, Electrical Engineering. New Mexico State University-Main Campus, Doctor of Phil...

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Math Tutors in Miami, French Tutors in Houston, Biology Tutors in New York City, Physics Tutors in Denver, Chemistry Tutors in Los Angeles, French Tutors in Phoenix, Biology Tutors in Dallas Fort Worth, MCAT Tutors in Miami, Algebra Tutors in Philadelphia, English Tutors in Dallas Fort Worth

Popular Courses & Classes

GRE Courses & Classes in Seattle, Spanish Courses & Classes in Los Angeles, SAT Courses & Classes in Seattle, Spanish Courses & Classes in Washington DC, ACT Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Atlanta, SAT Courses & Classes in New York City, Spanish Courses & Classes in Miami, ISEE Courses & Classes in Los Angeles

Popular Test Prep

GRE Test Prep in Seattle, MCAT Test Prep in San Francisco-Bay Area, GMAT Test Prep in San Diego, LSAT Test Prep in Atlanta, GRE Test Prep in Philadelphia, SSAT Test Prep in Washington DC, GMAT Test Prep in Boston, SAT Test Prep in Atlanta, ISEE Test Prep in Boston, SSAT Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Calculus II — Integrals

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : Using Limits With Continuity

Example Question #2 : Using Limits With Continuity

Example Question #3 : Calculus Ii — Integrals

Example Question #1 : Limits

Example Question #1 : Understanding Polar Coordinates

Example Question #2 : Understanding Polar Coordinates

Example Question #1 : Polar

Example Question #1 : Calculus Ii — Integrals

Example Question #5 : Parametric, Polar, And Vector

Example Question #6 : Parametric, Polar, And Vector

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: