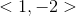All High School Math Resources
Example Questions
Example Question #1 : Limits

The above graph depicts a function 















Example Question #2 : Limits

The above graph depicts a function 











the actual value of )

As can be seen,


therefore, 
and 
Example Question #1 : Calculus Ii — Integrals
A function is defined by the following piecewise equation:
At 
discontinuous
continuous
continuous
The first step to determine continuity at a point is to determine if the function is defined at that point. When we substitute in 3 for 


The next step is determine if the limit of the function is defined at that point. This means that the left-hand limit must be equal to the right-hand limit at 
Both sides of the function, therefore, approach a 
Finally, we must ensure that the curve is smooth by checking the limit of the derivative of both sides.
Since the function passes all three tests, it is continuous.
Example Question #3 : Limits

The graph depicts a function 


















As can be seen, 



Example Question #1 : Calculus Ii — Integrals
The polar coordinates of a point are 

Given the polar coordinates 



Example Question #1 : Understanding Polar Coordinates
The polar coordinates of a point are 

Given the polar coordinates 



Example Question #1 : Parametric, Polar, And Vector
The polar coordinates of a point are 

Given the polar coordinates 



Example Question #2 : Parametric, Polar, And Vector
The polar coordinates of a point are 

Given the polar coordinates 



Example Question #1 : Calculus Ii — Integrals
Find the vector where its initial point is 

We need to subtract the 

Initial pt:
Terminal pt:
Vector:
Vector:
Example Question #1 : Vector
Find the vector where its initial point is 

We need to subtract the 

Initial pt:
Terminal pt:
Vector:
Vector:
Certified Tutor
All High School Math Resources