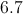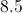A square is comprised of two 45-45-90 right triangles. The hypotenuse of a 45-45-90 right triangle follows the rule below, where \(\displaystyle x\) is the length of the sides. 

\(\displaystyle hypotenuse=x\sqrt2\)

In this instance, \(\displaystyle x\) is equal to 6.

\(\displaystyle hypotenuse=6\sqrt2=8.5\)

To find the diagonal of the square, we effectively cut the square into two \(\displaystyle 45^\circ:45^\circ:90^\circ\) triangles.

The pattern for the sides of a \(\displaystyle 45^\circ:45^\circ:90^\circ\) is \(\displaystyle x:x:x\sqrt{2}\).

Since two sides are equal to \(\displaystyle 5\), this triangle will have sides of \(\displaystyle 5:5:5\sqrt{2}\).

Therefore, the diagonal (the hypotenuse) will have a length of \(\displaystyle 5\sqrt{2}\).

To find the diagonal of a square, we must use the side length to create a 90 degree triangle with side lengths of \(\displaystyle 8\), \(\displaystyle 8\), and a hypotenuse which is equal to the diagonal.

Pythagorean’s Theorem states , where a and b are the legs and c is the hypotenuse.

Take \(\displaystyle 8\) and \(\displaystyle 8\) and plug them into the equation for \(\displaystyle a\) and \(\displaystyle b\): \(\displaystyle 8^{2}+8^{2}=c^{2}\)

After squaring the numbers, add them together: \(\displaystyle 64+64=128\)

Once you have the sum, take the square root of both sides: \(\displaystyle \sqrt{c^{2}}=\sqrt{128}\)

Simplify to find the answer: \(\displaystyle \sqrt{128}\), or \(\displaystyle 8\sqrt{2}\).

To find the diagonal of a square we must use the side lengths to create a 90 degree triangle with side lengths of 7 and a hypotenuse which is equal to the diagonal.

We can use the Pythagorean Theorem here to solve for the hypotenuse of a right triangle.

The Pythagorean Theorem states , where a and b are the sidelengths and c is the hypotenuse.

Plug the side lengths into the equation as \(\displaystyle a\) and \(\displaystyle b\):

\(\displaystyle 7^{2}+7^{2}=c^{2}\)

Square the numbers:

\(\displaystyle 49+49=c^{2}\)

Add the terms on the left side of the equation together:

\(\displaystyle 98=c^{2}\)

Take the square root of both sides:

\(\displaystyle \sqrt{98}=\sqrt{c^{2}}\)

 \(\displaystyle 9.9=c\)

Therefore the length of the diagonal is 9.9.

Perimeter = side * 4

48 = side * 4

Side = 12

We can break up the square into two equal right triangles. The diagonal of the sqaure is then the hypotenuse of these two triangles.

Therefore, we can use the Pythagorean Theorem to solve for the diagonal:

\(\displaystyle side^2 + side^2 = hypotenuse^2\)

\(\displaystyle 12^2+12^2=hypotenuse^2\)

\(\displaystyle 144 + 144=hypotenuse^2\)

\(\displaystyle \sqrt{144+144}=\sqrt{hypotenuse^2}\)

\(\displaystyle hypotenuse=\sqrt{2\times 144}=\sqrt{2\times 12\times 12}=12\sqrt{2}\)