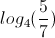We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Logarithms

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Logarithms

$\log_7118=?$

Possible Answers:

0.06

2.45

16.86

0.56

1.92

Correct answer:

2.45

Explanation:

Most of us don't know what the exponent would be if 7^x=118 and unfortunately there is no $\log_7$ on a graphing calculator -- only $\log$ (which stands for $\log_{10}$ ).

Fortunately we can use the base change rule: $\log_ba=\frac{\log_{10}a}{\log_{10}b}$

Plug in our given values.

$\log_7118=\frac{\log_{10}118}{\log_{10}7}$

$\log_7118=\frac{2.07}{0.845}$

$\log_7118=2.45$

Report an Error

Example Question #1 : Logarithms

Based on the definition of logarithms, what is ${\log_{10}1000}$ ?

Possible Answers:

100

Correct answer:

Explanation:

For any equation $\log_{10}(y) = x$ , $10^{x } = y$ . Thus, we are trying to determine what power of 10 is 1000. 1000 = 10^3 , so our answer is 3.

Report an Error

Example Question #2 : Logarithms

What is the value of that satisfies the equation $\log_x128=7$ ?

Possible Answers:

$\frac{1}{2}$

Correct answer:

Explanation:

$\log_xa=b$ is equivalent to x^b=a . In this case, you know the value of (the argument of a logarithmic equation) and b (the answer to the logarithmic equation). You must find a solution for the base.

$x^{7}=128$

$\sqrt[7]{x}=\sqrt[7]{128}$

x=2

Report an Error

Example Question #1 : Simplifying Logarithms

Simplify $log_{5}75 - log_{5}3$ .

Possible Answers:

0.75

1.50

Correct answer:

Explanation:

Using properties of logs we get:

$log_{5}75 - log_{5}3 = log_{5}\frac{75}{3}= log_{5}25$

$log_{5}25= log_{5}5^{2}= 2log_{5}5= 2\cdot 1=2$

Report an Error

Example Question #1 : Simplifying Logarithms

Simplify the following expression:

log(4) + log(12)

Possible Answers:

log(16)

log(48)

log(8)

log(3)

Correct answer:

log(48)

Explanation:

Recall the log rule:

log(a) + log(b) = log(ab)

In this particular case, a = 4 and b = 12 . Thus, our answer is $log(4\cdot 12) = log(48)$ .

Report an Error

Example Question #1 : Simplifying Logarithms

Use the properties of logarithms to solve the following equation:

$log_{6}(n-3)+log_{6}(n+2)=log_{3}(3)$

Possible Answers:

n=-3

n=4

n=3

n=-4

No real solutions

Correct answer:

n=4

Explanation:

Since the bases of the logs are the same and the logarithms are added, the arguments can be multiplied together. We then simplify the right side of the equation:

$log_{6}(n-3)+log_{6}(n+2)=log_{3}(3)$

$log_{6}(n-3)(n+2)=1$

The logarithm can be converted to exponential form:

$(n-3)(n+2)=6^{1}$

n^2-n-6=6

n^2-n-12=0

Factor the equation:

(n-4)(n+3)=0

n=4

Although there are two solutions to the equation, logarithms cannot be negative. Therefore, the only real solution is .

Report an Error

Example Question #1 : Simplifying Logarithms

Which of the following represents a simplified form of log(5x) ?

Possible Answers:

log(5)^x

5 * log(x)

log(5) + log(x)

log(5) * log(x)

$\frac{log(5) }{ log(x) }$

Correct answer:

log(5) + log(x)

Explanation:

The rule for the addition of logarithms is as follows:

log(ab) = log(a)+log(b) .

As an application of this, log(5x) = log(5)+log(x) .

Report an Error

Example Question #1 : Logarithms

Simplify the expression using logarithmic identities.

log_47-log_45

Possible Answers:

$log_4(\frac{5}{7})$

log_4(35)

The expression cannot be simplified

$log_4(\frac{7}{5})$

log_4(2)

Correct answer:

$log_4(\frac{7}{5})$

Explanation:

The logarithm of a fraction is equal to the logarithm of the numerator minus the logarithm of the denominator.

$log_A(\frac{B}{C})=log_AB-log_AC$

If we encounter two logarithms with the same base, we can likely combine them. In this case, we can use the reverse of the above identity.

$log_AB-log_AC=log_A(\frac{B}{C})$

$A=4,\ B=7,\ C=5$

$log_47-log_45=log_4(\frac{7}{5})$

Report an Error

Example Question #2 : Simplifying Logarithms

Evaluate by hand $\log_2(4^{\log_2(4^{5})})$

Possible Answers:

Cannot be found by hand

Correct answer:

Explanation:

Using the logarithm rules, exponents within logarithms can be removed and simply multiplied by the remaining logarithm. This expression can be simplified as $5\log_2(4)\log_2(4)$

Report an Error

Example Question #1 : Simplifying Logarithms

Solve for

log 2^x = 6

Possible Answers:

19.93

-8.6562

1.5897

Correct answer:

19.93

Explanation:

log 2^x = 6

Use the power reducing theorem:

$\log a^x = b \rightarrow x\log a = b$

a=2 and b=6

$x\log 2 = 6$

$x= \frac{6}{\log 2}$

x=19.93

Report an Error

View Tutors

Stephen
Certified Tutor

SUNY at Albany, Bachelor in Arts, Spanish. SUNY at Albany, Bachelor in Arts, Russian.

View Tutors

Lillian
Certified Tutor

University of the West Indies, Bachelor of Education, Elementary School Teaching.

View Tutors

Raynette
Certified Tutor

Boise State University, Bachelor in Arts, Elementary School Teaching. Colorado Christian University, Master of Arts, Counselo...

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Math Tutors in Miami, English Tutors in Atlanta, Calculus Tutors in Dallas Fort Worth, MCAT Tutors in Dallas Fort Worth, Physics Tutors in Chicago, Statistics Tutors in Phoenix, GRE Tutors in San Francisco-Bay Area, SSAT Tutors in Boston, Biology Tutors in Washington DC, Algebra Tutors in Boston

Popular Courses & Classes

LSAT Courses & Classes in Boston, ISEE Courses & Classes in New York City, SAT Courses & Classes in Houston, SSAT Courses & Classes in Denver, MCAT Courses & Classes in Boston, MCAT Courses & Classes in Philadelphia, MCAT Courses & Classes in Chicago, GRE Courses & Classes in Miami, ISEE Courses & Classes in San Diego, GRE Courses & Classes in San Francisco-Bay Area

Popular Test Prep

GRE Test Prep in Atlanta, SAT Test Prep in Atlanta, MCAT Test Prep in Atlanta, MCAT Test Prep in Chicago, SSAT Test Prep in New York City, LSAT Test Prep in Miami, GRE Test Prep in Denver, GMAT Test Prep in Boston, SSAT Test Prep in Washington DC, ISEE Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Logarithms

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : Logarithms

Example Question #1 : Logarithms

Example Question #2 : Logarithms

Example Question #1 : Simplifying Logarithms

Example Question #1 : Simplifying Logarithms

Example Question #1 : Simplifying Logarithms

Example Question #1 : Simplifying Logarithms

Example Question #1 : Logarithms

Example Question #2 : Simplifying Logarithms

Example Question #1 : Simplifying Logarithms

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: