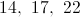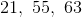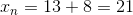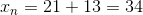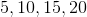Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Summations and Sequences

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Summations And Sequences

Consider the Fibonacci sequence written below. What are the next three terms?

$\small 1,\1,\ 2,\ 3,\ 5,\ 8,\ 13,...$ $\displaystyle \small 1,\1,\ 2,\ 3,\ 5,\ 8,\ 13,...$

Possible Answers:

$18, \23,\ 28$ $\displaystyle 18, \23,\ 28$

$14,\ 17 ,\ 22$ $\displaystyle 14,\ 17 ,\ 22$

$16,\ 21,\ 24$ $\displaystyle 16,\ 21,\ 24$

$21,\ 55,\ 63$ $\displaystyle 21,\ 55,\ 63$

$21,\ 34,\ 55$ $\displaystyle 21,\ 34,\ 55$

Correct answer:

$21,\ 34,\ 55$ $\displaystyle 21,\ 34,\ 55$

Explanation:

Each number in the Fibonacci sequence can be calculated by the sum of the previous two numbers.

$x_n=x_{n-1}+x_{n-2}$ $\displaystyle x_n=x_{n-1}+x_{n-2}$

The next term in the sequence will be the sum of the two terms preceding it: 8 and 13.

$\displaystyle x_n=13+8=21$

$\small 1,\1,\ 2,\ 3,\ 5,\ 8,\ 13,\ 21...$ $\displaystyle \small 1,\1,\ 2,\ 3,\ 5,\ 8,\ 13,\ 21...$

The next term will be the sum of 13 and 21.

$\displaystyle x_n=21+13=34$

$\small 1,\1,\ 2,\ 3,\ 5,\ 8,\ 13,\ 21,\ 34...$ $\displaystyle \small 1,\1,\ 2,\ 3,\ 5,\ 8,\ 13,\ 21,\ 34...$

The next term will be the sum of 21 and 34.

$\displaystyle x_n=34+21=55$

$\small 1,\1,\ 2,\ 3,\ 5,\ 8,\ 13,\ 21,\ 34,\ 55...$ $\displaystyle \small 1,\1,\ 2,\ 3,\ 5,\ 8,\ 13,\ 21,\ 34,\ 55...$

Report an Error

Example Question #1 : Mathematical Relationships And Basic Graphs

Which of the following is a geometric sequence?

Possible Answers:

$t_{0}=10$ $\displaystyle t_{0}=10$

$t_{n}=t_{n-1}+5$ $\displaystyle t_{n}=t_{n-1}+5$

$t_{0}=2$ $\displaystyle t_{0}=2$

$t_{n} = t_{n-1}^{6}$ $\displaystyle t_{n} = t_{n-1}^{6}$

$t_{0}=4$ $\displaystyle t_{0}=4$

$t_{n}=t_{n-1}+3.4$ $\displaystyle t_{n}=t_{n-1}+3.4$

$t_{0}=4$ $\displaystyle t_{0}=4$

$t_{n}=t_{n-1}\times 3$ $\displaystyle t_{n}=t_{n-1}\times 3$

$t_{0}=5$ $\displaystyle t_{0}=5$

$t_{n}=t_{n-1}+3$ $\displaystyle t_{n}=t_{n-1}+3$

Correct answer:

$t_{0}=4$ $\displaystyle t_{0}=4$

$t_{n}=t_{n-1}\times 3$ $\displaystyle t_{n}=t_{n-1}\times 3$

Explanation:

A geometric sequence is one in which the next term is found by mutlplying the previous term by a particular constant. Thus, we look for an implicit definition which involves multiplication of the previous term. The only possibility is:

$t_{0}=4$ $\displaystyle t_{0}=4$

$t_{n}=t_{n-1}\times 3$ $\displaystyle t_{n}=t_{n-1}\times 3$

Report an Error

Example Question #1 : Arithmetic Series

List the first 4 terms of an arithmetic sequence with a first term of 3, and a common difference of 5.

Possible Answers:

$\displaystyle 5, 10, 15, 20$

$\displaystyle 5, 8, 10, 13$

$\displaystyle 3, 8, 13, 18$

Correct answer:

$\displaystyle 3, 8, 13, 18$

Explanation:

An arithmetic sequence is one in which the common difference is added to one term to get the next term. Thus, if the first term is 3, we add 5 to get the second term, and continue in this manner.

Thus, the first four terms are:

$\displaystyle 3, 8, 13, 18$

Report an Error

View Tutors

Katelin
Certified Tutor

Vanderbilt University, Bachelor of Science, Human Resources Development. University of Miami School of Law, Professional (JD,...

View Tutors

Eva
Certified Tutor

Technicka Univerzita Liberec, Bachelor of Education, Education.

View Tutors

Chukwudi
Certified Tutor

University of Nigeria, Nsukka., Bachelor of Science, Biochemistry. African University of Science and Technology., Master of S...

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

French Tutors in Los Angeles, SAT Tutors in San Francisco-Bay Area, English Tutors in Dallas Fort Worth, Physics Tutors in San Francisco-Bay Area, Physics Tutors in Atlanta, Reading Tutors in Seattle, Computer Science Tutors in San Diego, GRE Tutors in Boston, SSAT Tutors in Boston, LSAT Tutors in Chicago

Popular Courses & Classes

LSAT Courses & Classes in Los Angeles, SAT Courses & Classes in Washington DC, SSAT Courses & Classes in New York City, Spanish Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in Seattle, LSAT Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Phoenix, ACT Courses & Classes in Seattle, ISEE Courses & Classes in Los Angeles, ISEE Courses & Classes in Washington DC

Popular Test Prep

GMAT Test Prep in Philadelphia, ACT Test Prep in Seattle, GRE Test Prep in Los Angeles, SAT Test Prep in Miami, LSAT Test Prep in San Francisco-Bay Area, ACT Test Prep in Boston, ISEE Test Prep in New York City, SSAT Test Prep in Philadelphia, GRE Test Prep in San Francisco-Bay Area, MCAT Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Summations and Sequences

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : Summations And Sequences

Example Question #1 : Mathematical Relationships And Basic Graphs

Example Question #1 : Arithmetic Series

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: