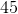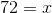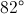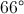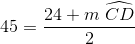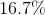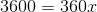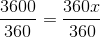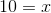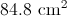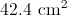Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Circles

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #21 : Geometry

A sector comprises 20% of a circle. What is the central angle of the sector?

Possible Answers:

Correct answer:

Explanation:

Proporations can be used to solve for the central angle. Let 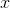equal the angle of the sector.

$\frac{20}{100}=\frac{x}{360}$

Cross mulitply:

7200=100x

Solve for :

$\frac{7200}{100}=\frac{100x}{100}$

72=x

Report an Error

Example Question #1 : Circles

Arcs

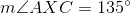
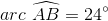
$m \angle AXC = 135^{\circ }$ ; $arc\ \widehat{AB} = 24^{\circ }$ ; $arc\ \widehat{AC} = 94^{\circ }$

Find the degree measure of $arc\ \widehat{CD}$ .

Possible Answers:

Not enough information is given to answer this question.

$82^{\circ}$

$132^{\circ }$

$66^{\circ }$

$164^{\circ}$

Correct answer:

$66^{\circ }$

Explanation:

When two chords of a circle intersect, the measure of the angle they form is half the sum of the measures of the arcs they intercept. Therefore,

$m \angle AXB = \frac{m\; \widehat{AB} + m\; \widehat{CD} }{2}$

Since $\angle AXB$ and $\angle AXC$ form a linear pair, $m \angle AXB + m \angle AXC = 180$ , and $m \angle AXB = 180 - m \angle AXC = 180 - 135 = 45^{\circ }$ .

Substitute $m\; \widehat{AB} = 24$ and $m \angle AXB = 45$ into the first equation:

$45 = \frac{24 + m\; \widehat{CD} }{2}$

$90 =24 + m\; \widehat{CD}$

$66 = m\; \widehat{CD}$

Report an Error

Example Question #3 : Circles

Two pizzas are made to the same dimensions. The only difference is that Pizza 1 is cut into pieces at 30° angles and Pizza 2 is cut at 45° angles. They are sold by the piece, the first for $1.95 per slice and the second for $2.25 per slice. What is the difference in total revenue between Pizza 2 and Pizza 1?

Possible Answers:

–$2.70

$5.40

–$5.40

$2.70

Correct answer:

–$5.40

Explanation:

First, let's calculate how many slices there are per pizza. This is done by dividing 360° by the respective slice degrees:

Pizza 1: 360/30 = 12 slices

Pizza 2: 360/45 = 8 slices

Now, the total amount made per pizza is calculated by multiplying the number of slices by the respective cost per slice:

Pizza 1: 12 * 1.95 = $23.40

Pizza 2: 8 * 2.25 = $18.00

The difference between Pizza 2 and Pizza 1 is thus represented by: 18 – 23.40 = –$5.40

Report an Error

Example Question #3 : Circles

What percentage of a full circle is the following sector? (Round to the nearest tenth of a percent.)

Arch

Note: The figure is not drawn to scale.

Possible Answers:

$14.4\%$

$20\%$

$16.7\%$

$25\%$

$33.3\%$

Correct answer:

$16.7\%$

Explanation:

In order to find the percentage of a sector from an angle, you need to know that a full circle is $360^{\circ}$ .

Therefore, we can find the percentage by dividing the angle of the sector by $360^{\circ}$ and then multiplying by 100:

$Percentage = \frac{\measuredangle}{360^{\circ}}\cdot 100$

$Percentage = \frac{60^{\circ}}{360^{\circ}}\cdot 100=\frac{1}{6}\cdot 100=.1\bar{6}\cdot 100=16.7\%$

Report an Error

Example Question #1 : Circles

A sector of a circle contains a center angle that is 36 degrees. What percentage of the circle is the sector?

Possible Answers:

$15\%$

$10\%$

$20\%$

$5\%$

Correct answer:

$10\%$

Explanation:

Proportions can be used to determine the percentage. Let equal the percentage comprised of the sector.

$\frac{36}{360}=\frac{x}{100}$

Cross multiply

3600=360x

Solve for x.

$\frac{3600}{360}=\frac{360x}{360}$

10=x

Report an Error

Example Question #1 : Circles

A circular, 8-slice pizza is placed in a square box that has dimensions four inches larger than the diameter of the pizza. If the box covers a surface area of 256 in², what is the surface area of one piece of pizza?

Possible Answers:

36π in²

18π in²

4.5π in²

9π in²

144π in²

Correct answer:

4.5π in²

Explanation:

The first thing to do is calculate the dimensions of the pizza box. Based on our data, we know 256 = s². Solving for s (by taking the square root of both sides), we get 16 = s (or s = 16).

Now, we know that the diameter of the pizza is four inches less than 16 inches. That is, it is 12 inches. Be careful! The area of the circle is given in terms of radius, which is half the diameter, or 6 inches. Therefore, the area of the pizza is π * 6² = 36π in². If the pizza is 8-slices, one slice is equal to 1/8 of the total pizza or (36π)/8 = 4.5π in².

Report an Error

Example Question #1 : Sectors

If B is a circle with line AC = 12 and line BC = 16, then what is the area formed by DBE?

Possible Answers:

$256\pi$

$100\pi$

$5\pi$

$200$

$144$

Correct answer:

$100\pi$

Explanation:

Line AB is a radius of Circle B, which can be found using the Pythagorean Theorem:

$AB^2=AC^2+BC^2\rightarrow AB=\sqrt{AC^2+BC^2}=\sqrt{16^2+12^2}=\sqrt{400}=20$

Since AB is a radius of B, we can find the area of circle B via:

$Area=\pi R^2=\pi(20^2)=400\pi$

Angle DBE is a right angle, and therefore $\frac{1}{4}$ of the circle so it follows:

$Area(DBE)=\frac{400}{4}\pi=100\pi$

Report an Error

Example Question #2 : Circles

To the nearest tenth, give the area of a $60^{\circ }$ sector of a circle with diameter 18 centimeters.

Possible Answers:

$84.8 \textrm{ cm}^{2}$

$169.6 \textrm{ cm}^{2}$

$254.5 \textrm{ cm}^{2}$

$21.2 \textrm{ cm}^{2}$

$42.4 \textrm{ cm}^{2}$

Correct answer:

$42.4 \textrm{ cm}^{2}$

Explanation:

The radius of a circle with diameter 18 centimeters is half that, or 9 centimeters. The area of a $60^{\circ }$ sector of the circle is

$A = \frac{60}{360 }\cdot \pi \cdot 9^{2} =\frac{1}{6} \cdot \pi \cdot 81 \approx 42.4 \textrm{ cm}^{2}$

Report an Error

Example Question #6 : Circles

Find the area of a sector that has an angle of 120 degrees and radius of 3.

Possible Answers:

$12\Pi$

$3\Pi$

$9\Pi$

$27\Pi$

$\frac{1}{3}\Pi$

Correct answer:

$3\Pi$

Explanation:

The equation to find the area of a sector is $(\frac{x}{360})\Pi r^2$ .

Substitute the given radius in for and the given angle in for to get:

$(\frac{120}{360})\Pi (3^2)$

Simplify the equation to get the area:

$(\frac{1}{3})\Pi9=3\Pi$

Report an Error

Example Question #5 : Circles

What is the area of the following sector of a full circle?

Arch

Note: Figure is not drawn to scale.

Possible Answers:

$21.5\pi m^2$

$27\pi m^2$

$23.5\pi m^2$

$10\pi m^2$

$13.5\pi m^2$

Correct answer:

$13.5\pi m^2$

Explanation:

In order to find the fraction of a sector from an angle, you need to know that a full circle is $360^{\circ}$ .

Therefore, we can find the fraction by dividing the angle of the sector by $360^{\circ}$ :

$Percentage = \frac{\measuredangle}{360^{\circ}}$

$Percentage = \frac{60^{\circ}}{360^{\circ}}=\frac{1}{6}$

The formula to find the area of a sector is:

$A=\pi (r^2)(fraction\ of\ whole\ circle)$

where is the radius of the circle.

Plugging in our values, we get:

$A=\pi (r^2)(fraction)$

$A=\pi (9m^2)\left(\frac{1}{6}\right)=13.5\pi m^2$

Report an Error

View Tutors

Daniel
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Psychology.

View Tutors

Aaron
Certified Tutor

Austin Peay State University, Bachelor, Education.

View Tutors

Traci
Certified Tutor

California State University-Fullerton, Bachelor of Science, History. UNLV, Masters in Education, Early Childhood Education.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Computer Science Tutors in Chicago, Spanish Tutors in Seattle, GMAT Tutors in Washington DC, ACT Tutors in Philadelphia, SAT Tutors in Houston, ISEE Tutors in Boston, Algebra Tutors in Phoenix, English Tutors in San Diego, Chemistry Tutors in Atlanta, SSAT Tutors in Dallas Fort Worth

Popular Courses & Classes

MCAT Courses & Classes in San Diego, SSAT Courses & Classes in Chicago, ACT Courses & Classes in Chicago, Spanish Courses & Classes in San Diego, MCAT Courses & Classes in Atlanta, GMAT Courses & Classes in Miami, ISEE Courses & Classes in Washington DC, SSAT Courses & Classes in Boston, ISEE Courses & Classes in Boston, SSAT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

SAT Test Prep in New York City, SAT Test Prep in Miami, ISEE Test Prep in Philadelphia, GMAT Test Prep in Phoenix, SSAT Test Prep in Houston, GRE Test Prep in Washington DC, MCAT Test Prep in Atlanta, SAT Test Prep in Los Angeles, ISEE Test Prep in Phoenix, SSAT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Circles

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #21 : Geometry

Example Question #1 : Circles

Example Question #3 : Circles

Example Question #3 : Circles

Example Question #1 : Circles

Example Question #1 : Circles

Example Question #1 : Sectors

Example Question #2 : Circles

Example Question #6 : Circles

Example Question #5 : Circles

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: