Funciones uno-a-uno
Una función f es 1-a-1 si no dos elementos en el dominio de f corresponden al mismo elemento en el rango de f . En otras palabras, cada x en el dominio tiene exactamente una imagen en el rango. Y, ninguna y en el rango es la imagen de más de una x en el dominio.
Si la gráfica de una función f es conocida, es fácil determinar si la función es 1-a-1. Use la prueba de la línea horizontal . Si ninguna línea horizontal intersecta la gráfica de la función f en más de un punto, entonces la función es 1-a-1.
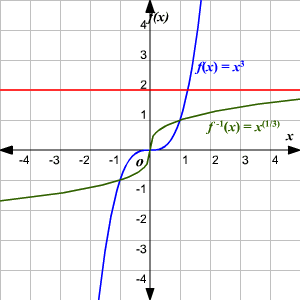
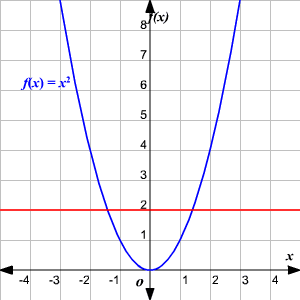
Una función f tiene una inversa f –1 (se lee f inversa de f ) si y solo si la función es 1-a-1.
Propiedades de una función 1-a-1:
1) El dominio de f es igual al rango de f –1 y el rango de f es igual al dominio de f –1 .
2) f –1 ( f ( x )) = x para cada x en el dominio de f y f ( f –1 ( x )) = x para cada x en el dominio de f –1 .
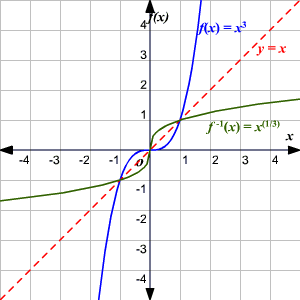
3) La gráfica de una función y la gráfica de su inversa son simétricas con respecto a la recta y = x.
- UK GCSE Chinese (Spoken Mandarin) Tutors
- German Lessons
- Narrative Production Tutors
- CIMA Courses & Classes
- Cantonese Tutors
- Arkansas Bar Exam Courses & Classes
- CFP Courses & Classes
- Series 22 Courses & Classes
- 8th Grade Homework Tutors
- CLEP Precalculus Test Prep
- ARM - Associate in Risk Management Test Prep
- UK A Level English Literature Tutors
- AP Computer Science A Tutors
- Music History Tutors
- GRE Subject Test in Psychology Courses & Classes
- DAT Test Prep
- German Courses & Classes
- CIMA Test Prep
- SAT Subject Test in Spanish Courses & Classes
- BCABA - Board Certified Assistant Behavior Analyst Test Prep