Resolviendo sistemas de ecuaciones lineales usando gráficas
Un sistema de ecuaciones lineales es solo un conjunto de dos o más ecuaciones lineales.
En dos variables ( x y y ), la gráfica de un sistema de dos ecuaciones es un par de rectas en el plano.
Hay tres posibilidades:
- Las rectas nunca se intersectan. (Las rectas son paralelas.)
- Las rectas se intersectan exactamente en un punto. (La mayoría de los casos.)
- Las rectas se intersectan infinitamente en muchos puntos. (Las dos ecuaciones representan la misma recta.)
Como resolver un sistema de ecuaciones usando el método gráfico
Este método es útil cuando solo necesita una respuesta aproximada, o está bastante seguro que la intersección ocurre en coordenadas enteras. Solo grafique las dos rectas, y vea donde se intersectan!
Ejemplo:
Resuelva el sistema graficando.
y = 0.5 x + 2
y = –2 x – 3
Las dos ecuaciones están en la forma intercepción-pendiente.
La primera recta tiene una pendiente de 0.5 y una intercepción en y de 2.
La segunda recta tiene una pendiente de −2 y una intercepción en y de −3.
Grafique las dos rectas como se muestra.
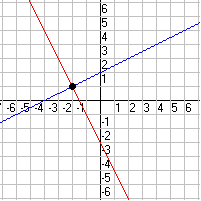
La solución es donde las dos rectas se intersectan, el punto (–2, 1). Esto es, x = −2 y y = 1.
- Anatomy Tutors
- FRM Test Prep
- WEST-E Test Prep
- Series 87 Courses & Classes
- CSET - California Subject Examinations for Teachers Test Prep
- Latin Tutors
- CLEP Humanities Courses & Classes
- Driver's Permit Exam Tutors
- Studio Art Tutors
- CompTIA Training
- CLEP College Composition Test Prep
- French Courses & Classes
- IB Information Technology in a Global Society HL Tutors
- CCNA Training
- CCNA Security Test Tutors
- LSW - Licensed Social Worker Courses & Classes
- AP Studio Art: 3-D Design Tutors
- PCAT Courses & Classes
- PMP Courses & Classes
- Differential Equations Tutors