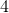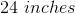ISEE Lower Level Quantitative : How to find symmetry
Study concepts, example questions & explanations for ISEE Lower Level Quantitative
All ISEE Lower Level Quantitative Resources
Example Questions
Example Question #1 : How To Find Symmetry
Find the average of the two endpoints to find their midpoint. To find the average of two numbers, add them together and divide by two.
Example Question #1 : Lines
How many lines of symmetry does a square have?
A line of symmetry is the imaginary line that you draw through a shape so that you can fold the image over the line and have both halves match exactly. Any regular shape has as many lines of symmetry as it does sides. Since a square has four sides, the correct answer is 4!
Example Question #2 : Lines
How many lines of symmetry does an octagon have?
A line of symmetry divides a shape into two equal and identical halves. Any regular shape has as many lines of symmetry as it does sides. Since octagons have eight sides, the correct answer is 8.
Example Question #4 : How To Find Symmetry Of A Line
How many lines of symmetry does a rectangle have?
A line of symmetry is the imaginary line that you draw through a shape so that you can fold the image over the line and have both halves match exactly. Any regular shape has as many lines of symmetry as it does total sides. Since a rectangle has four sides, the correct answer is 4!
Example Question #1 : How To Find Symmetry
The length of a certain line is 
Divide the length of the line by 2 to find the length of each half:
Example Question #2 : How To Find Symmetry
How many lines of symmetry does an octagon have?
A line of symmetry is the imaginary line that you draw through a shape so that you can fold the image over the line and have both halves match exactly. Any regular shape has as many lines of symmetry as it does sides. Since an octagon has eight sides, the correct answer is 
Example Question #12 : Lines
Ms. Johnson is knitting a blanket for her grandson. She has a piece of yarn that is exactly 
Ms. Johnson started with 
To find the length of the amount of yarn that she needs, divide 
The solution is:
Example Question #11 : Lines
Mr. Thomas' rectangular garden has a width of 
The length of Mr. Thomas' garden is exactly half the distance of the width of the garden.
The width of the garden is 
Thus, the length is equal to,
Example Question #3 : How To Find Symmetry
Celeste is Debra's 
Debra is 
Thus, to find Celeste's height, divide 
The solution is:
Step one: convert 
Step two: divide 
Step three: express 
Example Question #12 : Lines
Mr. Lam is planning on painting a rectangular wall in his living room. Before he starts painting, he decided to take a few measurements of the wall. He finds out that the width of the wall is twice the measurement of the height of the wall. If the width of the wall is 
Since the height of the rectangular wall is half the length of the width, divide 
The solution is:
Check:
Certified Tutor
Certified Tutor
All ISEE Lower Level Quantitative Resources
