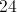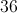We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

ISEE Lower Level Quantitative : Squares

Study concepts, example questions & explanations for ISEE Lower Level Quantitative

Create An Account

All ISEE Lower Level Quantitative Resources

20 Diagnostic Tests 114 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Squares

What is the area of a square if one side of the square is 6?

Possible Answers:

Correct answer:

Explanation:

If one side of a square is 6, then each of the four sides of the square are equal to 6. To find the area of a square, we multiply the length and the height together. The length is 6, and the height is 6, thus the equation we use is 6*6=36 .

Remember the formula for the area of a quadrilateral is length*width . For a square, one side is equal to both the length and the width.

Report an Error

Example Question #2 : Squares

One side of a square is centimeters long. What is the area of the square?

Possible Answers:

$64\: cm^{2}$

$8\: cm^{2}$

$16\: cm^{2}$

$32\: cm^{2}$

Correct answer:

$16\: cm^{2}$

Explanation:

The formula for finding the area of a square is $area = base\times height$ , or, because this is a square, $area = side^{2}$ .

area = centimeters $\times 4$ centimeters, or $16\: cm^{2}$

Report an Error

Example Question #3 : Squares

A right triangle has a base of and a height of .

What is the area of the rectangle made by 2 of these triangles aligned along the hypotenuse?

Possible Answers:

Correct answer:

Explanation:

If one combines the 2 identical triangles, their base and height become the length and width of the rectangle.

Area of a rectangle is:

$length\times height$

In this case

$7\times 4=28$

Report an Error

Example Question #4 : Squares

A square has an area of $16\ in^{2}$ . What is the length of one side?

Possible Answers:

$\dpi{100} 4\ inches$

$\dpi{100} 16\ inches$

$\dpi{100} 2\ inches$

$\dpi{100} 8\ inches$

Correct answer:

$\dpi{100} 4\ inches$

Explanation:

You can find the area of a square by multiplying two sides together. All of the sides of a square are equal. In this case, $\dpi{100} 4\times 4=16$ , so the length of all of the sides of the square is 4 inches.

Report an Error

Example Question #5 : Squares

Michaela drew th square below.

Screenshot_2015-03-25_at_3.13.25_pm

What is the area of the square?

Possible Answers:

100 square centimeters

12 square centimeters

112 square centimeters

144 square centimeters

48 square centimeters

Correct answer:

144 square centimeters

Explanation:

The area of a square can be found by multiplying the length of a side times itself. The side length of the above square is 12 cm. By finding 12 x 12, we find that the area of the square is 144 cm. squared.

Report an Error

Example Question #6 : Squares

James found the area of the square below to be 36 centimeters squared.

Screenshot_2015-03-25_at_3.13.12_pm

What is the length of one side of the square?

Possible Answers:

6 centimeters

9 centimeters

18 centimeters

8 centimeters

36 centimeters

Correct answer:

6 centimeters

Explanation:

The area of a square can be found by multiplying the length of a side by itself. 36 is equal to 6 times 6, therefore the length of one side is 6 centimeters.

Report an Error

Example Question #7 : Squares

Daphne found the area of the square below to be 81 centimeters squared.

Screenshot_2015-03-25_at_3.13.12_pm

What is the length of one side of the square?

Possible Answers:

9 centimeters

7 centimeters

20 centimeters

8 centimeters

81 centimeters

Correct answer:

9 centimeters

Explanation:

The area of a square can be found by multiplying the length of a side by itself. 81 is equal to 9 times 9, therefore the length of one side is 9 centimeters.

Report an Error

Example Question #8 : Squares

If the area of a square is $\small 36 ft^{2}$ , what is the length of each side?

Possible Answers:

$\small 7 ft$

$\small 9 ft$

$\small 6 ft$

$\small 10 ft$

$\small 13 ft$

Correct answer:

$\small 6 ft$

Explanation:

To find the area of a square, the length must be multiplied by the height. Since a square has four equal sides, the length and width will have the same measurement. We must, therefore, find the square root of $\small 36$ . Since $\small 6\cdot 6=36$ , $\small 6$ is the square root of $\small 36$ , which makes it the measurement for both the length and the width of the square.

Report an Error

Example Question #7 : Squares

If the length of a rectangle is four times the width, and the width is $\small 17 in$ , what is the perimeter of the rectangle?

Possible Answers:

$\small 68 in$

$\small 136 in$

$\small 170 in$

$\small 34 in$

$\small 140 in$

Correct answer:

$\small 170 in$

Explanation:

In order to find the perimeter of a rectangle, we must add the length of all the sides together. In this case, however, we must first determine the length, which can be found by multiplying $\small 4$ by $\small 17 in$ , because the length is four times the width, which had already been defined as $\small 17 in$ .

$\small \small \small 4\cdot 17 in=68in$

Now we add together the four sides.

$\small 68in+68in+17in+17in=170in$

Report an Error

Example Question #9 : Squares

If the perimeter of a square is $\small 116cm$ , what is the length of each side?

Possible Answers:

$\small 10cm$

$\small 27cm$

$\small 29cm$

$\small 24cm$

$\small 28cm$

Correct answer:

$\small 29cm$

Explanation:

To find the perimeter of a square, all the sides must be added together. Since a square has $\small 4$ equal sides, the length of each side can be determined by dividing the perimeter ( $\small 116cm$ ) by $\small 4$ .

$\small 116cm/4=29cm$

Report an Error

View Tutors

Pamela
Certified Tutor

University of Colorado Boulder, Bachelor of Science, International Marketing.

View Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

View Tutors

Ericka
Certified Tutor

Southern Nazarene University, Bachelors, Network Engineering and Management . Oklahoma State University-Main Campus, Master o...

All ISEE Lower Level Quantitative Resources

20 Diagnostic Tests 114 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

LSAT Tutors in Boston, Math Tutors in Philadelphia, Chemistry Tutors in Atlanta, Calculus Tutors in Atlanta, MCAT Tutors in Seattle, Computer Science Tutors in Philadelphia, LSAT Tutors in Miami, SAT Tutors in San Diego, ISEE Tutors in San Francisco-Bay Area, ISEE Tutors in Boston

Popular Courses & Classes

MCAT Courses & Classes in New York City, MCAT Courses & Classes in Boston, Spanish Courses & Classes in Philadelphia, GRE Courses & Classes in Seattle, Spanish Courses & Classes in San Diego, GMAT Courses & Classes in New York City, MCAT Courses & Classes in Washington DC, GRE Courses & Classes in Atlanta, GRE Courses & Classes in Philadelphia, ISEE Courses & Classes in Seattle

Popular Test Prep

MCAT Test Prep in Houston, MCAT Test Prep in Boston, GMAT Test Prep in Atlanta, SSAT Test Prep in San Diego, LSAT Test Prep in Dallas Fort Worth, GRE Test Prep in San Francisco-Bay Area, LSAT Test Prep in Miami, SAT Test Prep in Miami, ISEE Test Prep in Los Angeles, SAT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ISEE Lower Level Quantitative : Squares

Study concepts, example questions & explanations for ISEE Lower Level Quantitative

All ISEE Lower Level Quantitative Resources

Example Questions

Example Question #1 : Squares

Example Question #2 : Squares

Example Question #3 : Squares

Example Question #4 : Squares

Example Question #5 : Squares

Example Question #6 : Squares

Example Question #7 : Squares

Example Question #8 : Squares

Example Question #7 : Squares

Example Question #9 : Squares

All ISEE Lower Level Quantitative Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: