We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Precalculus : Write the Equation of a Polynomial Function Based on Its Graph

Study concepts, example questions & explanations for Precalculus

Create An Account

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Write The Equation Of A Polynomial Function Based On Its Graph

Which could be the equation for this graph?

Polynomial

Possible Answers:

y=2x^3 -7x^2 -21x + 54

y=-2x^3 +7x^2 +21x -54

y=-2x^3 -7x^2 + 21x + 54

y=2x^3 +7x^2 -21x -54

y=2x^3-x^4+2x-1

Correct answer:

y=-2x^3 -7x^2 + 21x + 54

Explanation:

This graph has zeros at 3, -2, and -4.5. This means that x-3=0 , x+2 =0 , and x+4.5=0 . That last root is easier to work with if we consider it as $x+\frac{9}{2}=0$ and simplify it to 2x+9=0 . Also, this is a negative polynomial, because it is decreasing, increasing, decreasing and not the other way around.

Our equation results from multiplying -(x-3)(x+2)(2x+9) , which results in -2x^3 -7x^2 +21x +54 .

Report an Error

Example Question #1 : Write The Equation Of A Polynomial Function Based On Its Graph

Write the quadratic function for the graph:

Varsity8

Possible Answers:

$f(x) = -x^{2} - 6x - 12$

$f(x) = x^{2} - 6x + 12$

$f(x) = -x^{2} - 12x + 3$

$f(x) = x^{2} + 12x + 3$

$f(x) = x^{2} + 6x - 12$

Correct answer:

$f(x) = x^{2} - 6x + 12$

Explanation:

Because there are no x-intercepts, use the form $f(x) = (x - h)^{2} + k$ , where vertex (h, k) is (3, 3) , so h = 3 , k = 3 , which gives

$f(x) = (x - 3)^{2} + 3$

= (x - 3)(x - 3) + 3

$= x^{2} + 2(-3)(x) + (-3)^{2} + 3$

$= x^{2} - 6x + 9 + 3$

$= x^{2} - 6x + 12$

Report an Error

Example Question #1 : Write The Equation Of A Polynomial Function Based On Its Graph

Write the quadratic function for the graph:

Varsity9

Possible Answers:

$f(x) = x^{2} - 6x - 2$

$f(x) = x^{2} - 8x + 12$

$f(x) = x^{2} - 4x + 12$

$f(x) = x^{2} + 8x + 12$

$f(x) = -6x^{2} - 4x - 2$

Correct answer:

$f(x) = x^{2} + 8x + 12$

Explanation:

Method 1:

The x-intercepts are x = -6, 2 . These values would be obtained if the original quadratic were factored, or reverse-FOILed and the factors were set equal to zero.

For x = -6 , x + 6 = 0 . For x = -2 , x + 2 = 0 . These equations determine the resulting factors and the resulting function; f(x) = (x + 6)(x + 2) .

Multiplying the factors and simplifying,

$f(x) = x\cdotx + 2\cdotx + 6\cdotx + 6\cdot2 = x^{2} + 8x + 12$ .

Answer: $f(x) = x^{2} + 8x + 12$ .

Method 2:

Use the form $(x - h)^{2} + k$ , where (h, k) is the vertex.

(h, k) is (-4, -4) , so h = -4 , k = -4 .

$(x - [-4])^{2} + (-4) = (x + 4)^{2} - 4$

Answer: $f(x) = (x + 4)^{2} - 4$

= (x + 4)(x + 4) - 4

$= x^{2} + 8x +16 - 4$

$= x^{2} + 8x + 12$

Report an Error

Example Question #2 : Write The Equation Of A Polynomial Function Based On Its Graph

Write the equation for the polynomial in this graph:

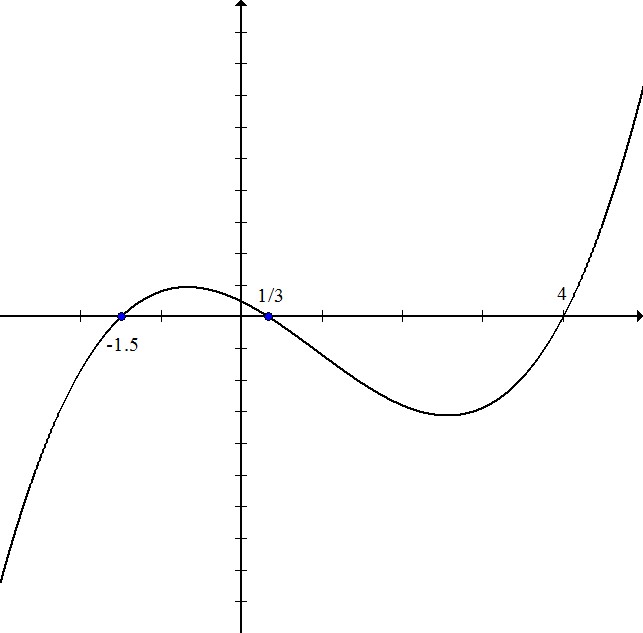
Graph 1 write funct

Possible Answers:

6x^3 -35x^2 + 47 x - 12

6x^3 + 17x^2 - 31 x - 12

6x^3 - 17x ^ 2 - 31 x + 12

6x^3 + 31 x^2 + 25 x - 12

6x^3 + 13 x ^ 2 - 41 x + 12

Correct answer:

6x^3 - 17x ^ 2 - 31 x + 12

Explanation:

The zeros for this polynomial are $-1.5, \frac{1}{3}, 4$ .

This means that the factors are equal to zero when these values are plugged in for x.

x + 1.5 = 0 multiply both sides by 2

2 x + 3 = 0 so one factor is 2x+3

$x - \frac{1}{3} = 0$ multiply both sides by 3

3x - 1 = 0 so one factor is 3x-1

x - 4 = 0 so one factor is x- 4

Multiply these three factors:

(2x+3) ( 3x-1) = 6x^2 + 9 x - 2 x - 3 = 6x^2 + 7 x - 3

$(6x^2 + 7 x - 3 ) ( x - 4 ) = 6x^3 + 7x^2 - 3 x \enspace -24x^2 - 28x + 12$ = 6x^3 - 17x^2 -31x+12

Report an Error

Example Question #1 : Write The Equation Of A Polynomial Function Based On Its Graph

Write the equation for the polynomial shown in this graph:

Graph 2 write funct

Possible Answers:

-2x^3 +3x^2 +32x+48

-2x^3 -3x^2 +32x+48

-2x^3 -13x^2 -8x+48

-2x^3 +19x ^2 -56x + 48

-2x^3 -19x^2 -56x-48

Correct answer:

-2x^3 -3x^2 +32x+48

Explanation:

The zeros of this polynomial are 4, -4 , -1.5 . This means that the factors equal zero when these values are plugged in.

One factor is x - 4

One factor is x + 4

The third factor is equivalent to x + 1.5 . Set equal to 0 and multiply by 2:

2(x + 1.5) = 2(0 )

2x+3 = 0

Multiply these three factors:

(x-4)(x+4) = x^2 - 16

(x^2 - 16) (2x+3 ) = 2x^3 +3x^2 - 32x - 48

The graph is negative since it goes down then up then down, so we have to switch all of the signs:

y = -2x^3 -3x^2 + 32x + 48

Report an Error

Example Question #1 : Write The Equation Of A Polynomial Function Based On Its Graph

Write the equation for the polynomial in the graph:

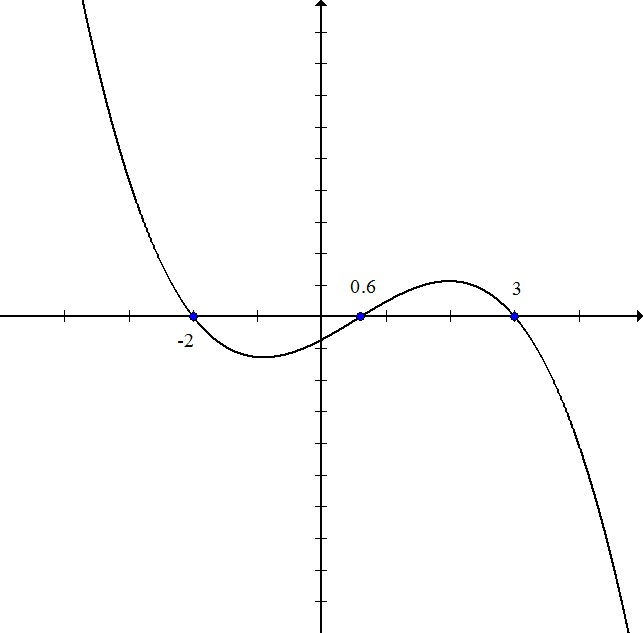
Graph 4 write funct

Possible Answers:

-5x^3 +8x^2 +27x-18

-5x^3 -2x^2 +33x -18

-5x^3 +28x^2 -45x +18

-5x^3 -8x^2 +27x +18

-5x^3 -22x^2 -15x + 18

Correct answer:

-5x^3 +8x^2 +27x-18

Explanation:

The zeros of the polynomial are 0.6, 3, -2 . That means that the factors equal zero when these values are plugged in.

The first factor is x - 0.6 = 0 or equivalently $x - \frac{3}{5} = 0$ multiply both sides by 5:

5x- 3 = 0

The second and third factors are x - 3 = 0 and x + 2 = 0

Multiply:

(5x - 3 ) ( x - 3 ) = 5x^2 -3x -15x +9 = 5x^2 -18x + 9

$(5x^2 -18x + 9 ) ( x + 2 ) = 5x^3 -18x^2 +9x \enspace + 10x^2 -36x +18$

= 5x^3 - 8x^2 -27x + 18

Because the graph goes down-up-down instead of the standard up-down-up, the graph is negative, so change all of the signs:

-5x^3 +8x^2 +27x - 18

Report an Error

Example Question #1 : Write The Equation Of A Polynomial Function Based On Its Graph

Write the equation for the polynomial in this graph:

Graph 3 write funct

Possible Answers:

12x^3 +23x^2 -93x + 28

12x^3 +65x^2 -61x-28

12x^3 + 31x^2 -75x -28

12x^3 -31x^2 -75x+28

12x^3 -73x^2 +107 x -28

Correct answer:

12x^3 -31x^2 -75x+28

Explanation:

The zeros for this polynomial are $-1.75, \frac{1}{3}, 4$ . That means that the factors are equal to zero when these values are plugged in.

x + 1.75 = 0 or equivalently $x + \frac{7}{4} = 0$ multiply both sides by 4

4x+7 = 0 the first factor is 4x+7

$x-\frac{1}{3} = 0$ multiply both sides by 3

3x-1 = 0 the second factor is 3x - 1

x - 4 = 0 the third factor is x - 4

Multiply the three factors:

(4x+7)(3x-1) = 12x^2 +21x -4x - 7 = 12x^2+ 17x - 7

$(12x^2 +17x - 7 )(x-4) = 12x^3 +17x^2 -7x + \enspace -48x^2 -68x +28$

= 12x^3 -31x^2 -75x +28

Report an Error

View Pre-Calculus Tutors

John
Certified Tutor

Arizona State University, Bachelor of Science, Microbiology.

View Pre-Calculus Tutors

Vandana
Certified Tutor

Jawaharlal Nehru Technological University, Bachelor of Technology, Civil Engineering. Florida International University, Maste...

View Pre-Calculus Tutors

Vicky
Certified Tutor

Clemson University, Doctor of Science, Civil Engineering.

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ISEE Tutors in Phoenix, MCAT Tutors in Chicago, Biology Tutors in San Francisco-Bay Area, Physics Tutors in Los Angeles, MCAT Tutors in Denver, GRE Tutors in Seattle, LSAT Tutors in Atlanta, GMAT Tutors in Atlanta, Algebra Tutors in Denver, LSAT Tutors in Chicago

Popular Courses & Classes

SAT Courses & Classes in Phoenix, ISEE Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Chicago, SSAT Courses & Classes in New York City, LSAT Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Miami, GRE Courses & Classes in Washington DC, SSAT Courses & Classes in Houston, SAT Courses & Classes in Denver, ACT Courses & Classes in Dallas Fort Worth

Popular Test Prep

GRE Test Prep in Miami, MCAT Test Prep in Miami, GMAT Test Prep in Boston, SAT Test Prep in Chicago, GRE Test Prep in Atlanta, ISEE Test Prep in Los Angeles, SSAT Test Prep in Philadelphia, SAT Test Prep in Los Angeles, MCAT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Precalculus : Write the Equation of a Polynomial Function Based on Its Graph

Study concepts, example questions & explanations for Precalculus

All Precalculus Resources

Example Questions

Example Question #1 : Write The Equation Of A Polynomial Function Based On Its Graph

Example Question #1 : Write The Equation Of A Polynomial Function Based On Its Graph

Example Question #1 : Write The Equation Of A Polynomial Function Based On Its Graph

Example Question #2 : Write The Equation Of A Polynomial Function Based On Its Graph

Example Question #1 : Write The Equation Of A Polynomial Function Based On Its Graph

Example Question #1 : Write The Equation Of A Polynomial Function Based On Its Graph

Example Question #1 : Write The Equation Of A Polynomial Function Based On Its Graph

All Precalculus Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: