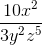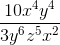Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : Variables

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Monomials

Multiply: (1-x^2)(9x)

Possible Answers:

9x^3-1

-1-9x^3

-x^2+9x+1

9x-9x^3

9x^3-9x

Correct answer:

9x-9x^3

Explanation:

Distribute the monomial through the polynomial.

(1-x^2)(9x)= 9x-9x^3

The answer is: 9x-9x^3

Report an Error

Example Question #1 : Variables

Evaluate: 3x(x^2+3x-1)

Possible Answers:

3x^3-9x^2+3x

3x^3+x^2-x

4x^3-6x-3x

3x^3+9x^2-3x

4x^3+6x-3x

Correct answer:

3x^3+9x^2-3x

Explanation:

Distribute the monomial through each term inside the parentheses.

3x(x^2+3x-1)= 3x(x^2)+(3x)(3x)+(3x)(-1)

= 3x^3+9x^2-3x

Report an Error

Example Question #2 : Variables

Multiply the monomials: $6x \times 4x^2$

Possible Answers:

$\textup{They are not like terms, so they can't be multiplied.}$

24x^3

48x^3

72x

24x^2

Correct answer:

24x^3

Explanation:

In order to multiply this, we can simply multiply the coefficients together and the variables together. Anytime we multiply a variable of the same base, we can add the exponents.

$6x \times 4x^2 = (6\cdot 4) (x^1\cdot x^2)$

Simplify the right side.

$(6\cdot 4) (x^1\cdot x^2) = 24(x^{1+2})= 24x^3$

The answer is: 24x^3

Report an Error

Example Question #1 : Variables

Distribute: 4ab(3a-5b+1)

Possible Answers:

-8ab-1

12a^2b-20ab^2

12a^2b+20ab^2+4ab

12a^2b-20ab^2+4ab

-8ab+1

Correct answer:

12a^2b-20ab^2+4ab

Explanation:

Distribute the monomial to each part of the polynomial, paying careful attention to signs:

4ab(3a-5b+1)

$4ab\cdot3a+4ab\cdot(-5b)+4ab\cdot1$

12a^2b-20ab^2+4ab

Report an Error

Example Question #2 : Monomials

Find the product:

$\left ( \frac{5x^3y^5}{y^6z^4} \right )\left ( \frac{2xy^{-1}}{3zx^2} \right )$

Possible Answers:

$\frac{10x^2}{3y^2z^5}$

$\frac{10x^3}{z^4}$

$\frac{x}{y^4}$

$\frac{5y^6}{2xz^4}$

x^2z^4

Correct answer:

$\frac{10x^2}{3y^2z^5}$

Explanation:

Find the product:

$\left ( \frac{5x^3y^5}{y^6z^4} \right )\left ( \frac{2xy^{-1}}{3zx^2} \right )$

Step 1: Multiply the numerators and denominators using the properties of exponents. (When multiplying exponents, add them.)

$\frac{5x^3y^5\cdot 2xy^{-1}}{y^6z^4\cdot 3zx^2}$

$\frac{10x^4y^4}{3y^6z^5x^2}$

Step 2: Simplify the expression.

$\frac{10x^2}{3y^2z^5}$

Report an Error

Example Question #1 : Direct And Inverse Variation

Phillip can paint square feet of wall per minute. What area of the wall can he paint in 2.5 hours?

Possible Answers:

$300y\ ft^2$

$25y\ ft^2$

$2.5y\ ft^2$

$50y\ ft^2$

$150y\ ft^2$

Correct answer:

$150y\ ft^2$

Explanation:

Every minute Phillip completes another square feet of painting. To solve for the total area that he completes, we need to find the number of minutes that he works.

There are 60 minutes in an hour, and he paints for 2.5 hours. Multiply to find the total number of minutes.

$(60\frac{min}{hr})(2.5hr)=150min$

If he completes square feet per minute, then we can multiply by the total minutes to find the final answer.

$(y\frac{ft^2}{min})(150min)=150y\ ft^2$

Report an Error

Example Question #1 : Direct And Inverse Variation

The value of varies directly with the square of and the cube of . If y=24 when x=1 and z=2 , then what is the value of when x=3 and z=1 ?

Possible Answers:

Correct answer:

Explanation:

Let's consider the general case when y varies directly with x. If y varies directly with x, then we can express their relationship to one another using the following formula:

y = kx, where k is a constant.

Therefore, if y varies directly as the square of x and the cube of z, we can write the following analagous equation:

y = kx²z³, where k is a constant.

The problem states that y = 24 when x = 1 and z = 2. We can use this information to solve for k by substituting the known values for y, x, and z.

24 = k(1)²(2)³ = k(1)(8) = 8k

24 = 8k

Divide both sides by 8.

3 = k

k = 3

Now that we have k, we can find y if we know x and z. The problem asks us to find y when x = 3 and z = 1. We will use our formula for direct variation again, this time substitute values for k, x, and z.

y = kx²z³

y = 3(3)²(1)³ = 3(9)(1) = 27

y = 27

The answer is 27.

Report an Error

Example Question #2 : Direct And Inverse Variation

In a growth period, a population of flies triples every week. If the original population had 3 flies, how big is the population after 4 weeks?

Possible Answers:

$81$

$243$

$27$

$729$

$2187$

Correct answer:

$243$

Explanation:

We know that the initial population is 3, and that every week the population will triple.

The equation to model this growth will be i(r)^n , where is the initial size, is the rate of growth, and is the time.

In this case, the equation will be 3(3)^4 .

3(3)^4=3(81)=243

Alternatively, you can evaluate for each consecutive week.

Week 1: 3(3)=9

Week 2: 3(9)=27

Week 3: 3(27)=81

Week 4: 3(81)=243

Report an Error

Example Question #8 : Variables

and are the diameter and circumference, respectively, of the same circle.

$d = 12L^{2}$

$C = t^{2}$

Which of the following is a true statement? (Assume all quantities are positive)

Possible Answers:

varies directly as .

varies directly as the fourth root of .

varies inversely as the fourth power of .

varies directly as the fourth power of .

varies inversely as the fourth root of .

Correct answer:

varies directly as .

Explanation:

If and are the diameter and circumference, respectively, of the same circle, then

$C = \pi d$ .

By substitution,

$t^{2} = \pi \cdot 12 L^{2}$

$t^{2} = 12 \pi L^{2}$

Taking the square root of both sides:

$\sqrt{t^{2} }= \sqrt{12 \pi L^{2}}$

$t = \sqrt{12 \pi} \cdot \sqrt{L^{2}}$

$t = \sqrt{12 \pi} \cdot L$

Taking $K= \sqrt{12 \pi}$ as the constant of variation, we get

t =K L ,

meaning that varies directly as .

Report an Error

Example Question #2 : How To Use The Direct Variation Formula

is the radius of the base of a cone; is its height; is its volume.

$n = 4r = h^{2}$ ; $m = V ^{2}$ .

Which of the following is a true statement?

Possible Answers:

varies directly as the cube root of .

varies directly as the third power of .

varies directly as .

varies directly as the fifth root of .

varies directly as the fifth power of .

Correct answer:

varies directly as the fifth power of .

Explanation:

The volume of a cone can be calculated from the radius of its base , and the height , using the formula

$V = \frac{1}{3} \pi r^{2}h$

n = 4r , so $r = \frac{n}{4}$ .

$n = h^{2}$ , so $h = \sqrt{n}$ .

$V = \frac{1}{3} \pi r^{2}h$ , so by substitution,

$V = \frac{1}{3} \pi\left ( \frac{n}{4} \right ) ^{2} \cdot \sqrt{n}$

$V = \frac{1}{3} \pi\left ( \frac{n^{2}}{16} \right ) \cdot \sqrt{n}$

$V = \frac{1}{48} \pi \cdot n^{2}} \sqrt{n}$

Square both sides:

$V ^{2 }=\left ( \frac{1}{48} \pi \cdot n^{2}} \sqrt{n} \right )^{2}$

$m=\left ( \frac{1}{48} \pi \right )^{2} \cdot \left ( n^{2}} \sqrt{n} \right )^{2}$

$m=\left ( \frac{1}{48} \pi \right )^{2} \cdot \left ( n^{2}} \right )^{2} \cdot \left ( \sqrt{n} \right )^{2}$

$m=\left ( \frac{1}{48} \pi \right )^{2} \cdot n^{4}} \cdot n$

$m=\left ( \frac{1}{48} \pi \right )^{2} \cdot n^{5}}$

If we take $K = \left ( \frac{1}{48} \pi \right )^{2}$ as the constant of variation, then

$m=K n^{5}}$ ,

and varies directly as the fifth power of .

Report an Error

View SAT Mathematics Tutors

Miriam
Certified Tutor

Washington University in St Louis, Bachelor in Arts, Biology, General.

View SAT Mathematics Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

View SAT Mathematics Tutors

Irina
Certified Tutor

New York University, Bachelors, Biochemistry.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

SSAT Courses & Classes in Houston, GRE Courses & Classes in San Diego, Spanish Courses & Classes in San Diego, GRE Courses & Classes in Seattle, LSAT Courses & Classes in Miami, GMAT Courses & Classes in Miami, LSAT Courses & Classes in Denver, Spanish Courses & Classes in Phoenix, SAT Courses & Classes in Chicago, LSAT Courses & Classes in Philadelphia

Popular Test Prep

LSAT Test Prep in Washington DC, MCAT Test Prep in Seattle, SAT Test Prep in New York City, LSAT Test Prep in San Francisco-Bay Area, MCAT Test Prep in Philadelphia, SAT Test Prep in Washington DC, SAT Test Prep in Chicago, SSAT Test Prep in Denver, SAT Test Prep in San Diego, SSAT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : Variables

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #1 : Monomials

Example Question #1 : Variables

Example Question #2 : Variables

Example Question #1 : Variables

Example Question #2 : Monomials

Example Question #1 : Direct And Inverse Variation

Example Question #1 : Direct And Inverse Variation

Example Question #2 : Direct And Inverse Variation

Example Question #8 : Variables

Example Question #2 : How To Use The Direct Variation Formula

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: