All 8th Grade Math Resources
Example Questions
Example Question #1 : 8th Grade Math
Which of the following answer choices displays a rational number?
Our answer choices consist of two types of numbers: rational numbers and irrational numbers. In order to correctly answer this question, we need to know the difference between the two types of numbers.
Rational numbers are numbers that we use most often, and can be written as a simple fraction.
Irrational numbers cannot be written as fractions, and are numbers that have decimal places that never repeat or end.
In this case, 
Example Question #2 : 8th Grade Math
Solve:
In order to solve this problem, we need to recall our exponent rules:
When our base numbers are equal to each other, like in this problem, we can add our exponents together using the following formula:
Let's apply this rule to our problem
Solve for the exponents
We cannot leave this problem in this format because we cannot have a negative exponent. Instead, we can move the base and the exponent to the denominator of a fraction:
Solve the problem
Example Question #1 : Algebra
Select the table that properly represents a function.





Each of the tables provided contains sets of ordered pairs. The input column represents the x-variables, and the output column represents the y-variables. We can tell if a set of ordered pairs represents a function when we match x-values to y-values.
In order for a table to represents a function, there must be one and only one input for every output. This means that our correct answer will have all unique input values:

Functions cannot have more than one input value that is the same; thus, the following tables do not represent a function:



Example Question #2 : Algebra
Select the equation that best represents a linear function.
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:
If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:

Notice that in this equation our 
Though this equation is not written in 

Again, though this equation is not written in 

For this equation, we can solve for 
First, we can subtract 
Next, we can divide each side by
This equation is in slope-intercept form; thus, 
Example Question #3 : Algebra
Use algebra to solve the following system of linear equations:
There are a couple of ways to solve a system of linear equations: graphically and algebraically. In this lesson, we will review the two ways to solve a system of linear equations algebraically: substitution and elimination.
Substitution can be used by solving one of the equations for either 


Elimination is best used when one of the variables has the same coefficient in both equations, because you can then use addition or subtraction to cancel one of the variables out, and solve for the other variable.
For this problem, substitution makes the most sense because the first equation is already solved for a variable. We can substitute the expression that is equal to 

Next, we need to distribute and combine like terms:
We are solving for the value of 


Then divide both sides by 
Remember, when we are solving a system of linear equations, we are looking for the point of intersection; thus, our answer should have both 

Now that we have the value of 

Our point of intersection, and the solution to the system of linear equations is 
Example Question #1 : Geometry
The image provided contains a set of parallel lines, 





First, we need to define some key terms:
Parallel Lines: Parallel lines are lines that will never intersect with each other.
Transversal Line: A transversal line is a line that crosses two parallel lines.
In the the image provided, lines 


It is important to know that transversal lines create angle relationships:
- Vertical angles are congruent
- Corresponding angles are congruent
- Alternate interior angles are congruent
- Alternate exterior angles are congruent
Let's look at angle 

Angle 

Angle 

Angle 

Angle 




For this problem, we want to find the angle that is congruent to angle 




Example Question #2 : Geometry
Calculate the length of the missing side of the provided triangle. Round the answer to the nearest whole number.

The provided triangle is a right triangle. We know this because the angle marker in the left corner of the triangle indicates that the triangle possesses a right or 
We can use the Pythagorean Theorem to help us solve this problem.
The Pythagorean Theorem states that for right triangles, the square of the hypotenuse is equal to the sum of the square of the other two sides. In other terms:

We can use the formula and substitute the known side lengths from the problem to solve for the missing side length:
Example Question #3 : Geometry
Calculate the volume of the cone provided. Round the answer to the nearest hundredth.

In order to solve this problem, we need to recall the formula used to calculate the volume of a cone:
Now that we have this formula, we can substitute in the given values and solve:
Example Question #3 : 8th Grade Math
The scatter plot provided displays a group of students' test scores versus the number of missing assignments the students have. Based on plot, select the best answer that describes the direction of the points.

A negative, non linear association
A positive, linear association
A negative, linear association
A positive, nonlinear association
A negative, linear association
The data points in the scatter plot move up the y-axis as the x-axis decreases; thus the data points show a negative association. Also, the data points do not curve, or go up and down, but gradually decreased; thus the scatter plot shows a linear association. We could even draw a "best fit" line:

Example Question #4 : 8th Grade Math
A teacher at a high school conducted a survey of seniors and found that 



To help answer this question, we can construct a two-way table and fill in our known quantities from the question.
The columns of the table will represent the students who have a laptop or do not have a laptop and the rows will contain the students who have a car or do not have a car. The first bit of information that we were given from the question was that 








Our question asked how many students have a laptop, but do not own have a car. We can take the total number of students that own a lap top, 
This means that 
All 8th Grade Math Resources

























![\frac{\begin{array}[b]{r}3y+12x=21\\ -12x-12x\end{array}}{\\\\3y=-12x+21}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/963514/gif.latex)












![\frac{\begin{array}[b]{r}15y+3=-27\\ \ -3\ \ \ \ -3\end{array}}{\\\\15y=-30}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/956490/gif.latex)


































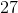


![\frac{\begin{array}[b]{r}81\\ -\ 54\end{array}}{ \ \ \ \space 27}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/980467/gif.latex)



