Call Now to Set Up Tutoring:

(888) 888-0446

8th Grade Math : Geometry

Study concepts, example questions & explanations for 8th Grade Math

Create An Account

All 8th Grade Math Resources

6 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Geometry

The image provided contains a set of parallel lines, $\overline{AB}$ and $\overline{CD}$ , and a transversal line, $\overline{EF}$ . If angle $\angle{\ a}$ is equal to $135^\circ$ , then which of the other angles is equal to $135^\circ?$

Possible Answers:

$\angle{\ c}$

$\angle{\ f}$

$\angle{\ b}$

$\angle{\ d}$

Correct answer:

$\angle{\ c}$

Explanation:

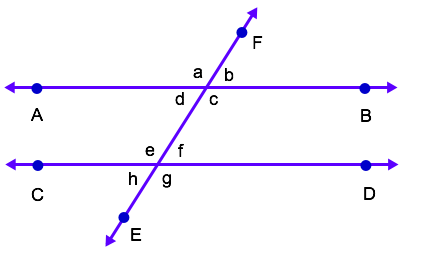
First, we need to define some key terms:

Parallel Lines: Parallel lines are lines that will never intersect with each other.

Transversal Line: A transversal line is a line that crosses two parallel lines.

In the the image provided, lines $\overline{AB}$ and $\overline{CD}$ are parallel lines and line $\overline{EF}$ is a transversal line because it crosses the two parallel lines.

It is important to know that transversal lines create angle relationships:

Vertical angles are congruent
Corresponding angles are congruent
Alternate interior angles are congruent
Alternate exterior angles are congruent

Let's look at angle $\angle{\ a}$ in the image provided below to demonstrate our relationships.

Angle $\angle{\ a}$ and $\angle{\ c}$ are vertical angles.

Angle $\angle{\ a}$ and $\angle{\ e}$ are corresponding angles.

Angle $\angle{\ a}$ and $\angle{\ g}$ are exterior angles.

Angle $\angle{\ a}$ is an exterior angle; therefore, it does not have an alternate interior angle. In this image, the alternate interior angles are the angle pairs $\angle{\ e}$ and $\angle{\ c}$ as well as angle $\angle{\ d}$ and $\angle{\ f}$ .

For this problem, we want to find the angle that is congruent to angle $\angle{\ a}$ . Based on our answer choices, angle $\angle{\ a}$ and $\angle{\ c}$ are vertical angles; thus, both angle $\angle{\ a}$ and $\angle{\ c}$ are congruent and equal $135^\circ$

Report an Error

Example Question #2 : Geometry

Calculate the length of the missing side of the provided triangle. Round the answer to the nearest whole number.

Possible Answers:

$35\textup{ cm}$

$34\textup{ cm}$

$37\textup{ cm}$

$36\textup{ cm}$

Correct answer:

$37\textup{ cm}$

Explanation:

The provided triangle is a right triangle. We know this because the angle marker in the left corner of the triangle indicates that the triangle possesses a right or $90^\circ$ angle. When a triangle includes a right angle, the triangle is said to be a "right triangle."

We can use the Pythagorean Theorem to help us solve this problem.

The Pythagorean Theorem states that for right triangles, the square of the hypotenuse is equal to the sum of the square of the other two sides. In other terms:

a^2+b^2=c^2

We can use the formula and substitute the known side lengths from the problem to solve for the missing side length:

12^2+35^2=c^2

$144+1\textup,225=c^2$

$1\textup,369=c^2$

$\sqrt{1\textup,369}=\sqrt{c^2}$

37=c

Report an Error

Example Question #3 : Geometry

Calculate the volume of the cone provided. Round the answer to the nearest hundredth.

Possible Answers:

$60.23\textup{ in}^3$

$56.55\textup{ in}^3$

$62.22\textup{ in}^3$

$58.45\textup{ in}^3$

Correct answer:

$56.55\textup{ in}^3$

Explanation:

In order to solve this problem, we need to recall the formula used to calculate the volume of a cone:

$V=\pi r^2\left ( \frac{h}{3} \right )$

Now that we have this formula, we can substitute in the given values and solve:

$V=\pi3^2\left ( \frac{6}{3} \right )$

$V=\pi9(2)$

$V=\pi18$

$V=56.55\textup{ in}^3$

Report an Error

View Tutors

Patricia
Certified Tutor

SUNY New Paltz, Bachelors, French. SUNY New Paltz, Masters, Secondary Education: French.

View Tutors

Anjali
Certified Tutor

Delhi University, Bachelor of Science, Physics. Kumuan University, Master of Science, Physics.

View Tutors

Pankaj
Certified Tutor

University of Delhi, Electrical Engineer, Electrical Engineering. Columbia University in the City of New York, Master of Arts...

All 8th Grade Math Resources

6 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

LSAT Tutors in Seattle, LSAT Tutors in Denver, Chemistry Tutors in Seattle, ACT Tutors in Phoenix, GMAT Tutors in San Diego, Algebra Tutors in Atlanta, ISEE Tutors in Dallas Fort Worth, SSAT Tutors in Chicago, GRE Tutors in Denver, Math Tutors in New York City

Popular Courses & Classes

ISEE Courses & Classes in New York City, SAT Courses & Classes in Denver, MCAT Courses & Classes in Chicago, Spanish Courses & Classes in Chicago, SAT Courses & Classes in Los Angeles, Spanish Courses & Classes in Miami, ISEE Courses & Classes in Los Angeles, LSAT Courses & Classes in Seattle, GMAT Courses & Classes in San Diego, SAT Courses & Classes in New York City

Popular Test Prep

MCAT Test Prep in San Francisco-Bay Area, MCAT Test Prep in Boston, ACT Test Prep in Atlanta, MCAT Test Prep in Atlanta, GMAT Test Prep in San Diego, SAT Test Prep in Los Angeles, GMAT Test Prep in Atlanta, SAT Test Prep in Atlanta, GMAT Test Prep in New York City, ACT Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

8th Grade Math : Geometry

Study concepts, example questions & explanations for 8th Grade Math

All 8th Grade Math Resources

Example Questions

Example Question #1 : Geometry

Example Question #2 : Geometry

Example Question #3 : Geometry

All 8th Grade Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: