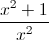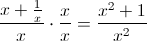ACT Math : How to find a complex fraction
Study concepts, example questions & explanations for ACT Math
All ACT Math Resources
Example Questions
Example Question #10 : Complex Fractions
Simplify
Simplify the complex fraction by multiplying by the complex denominator:
Example Question #3 : How To Add And Subtract Fractions
Steven purchased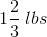 
To solve this answer, we have to first make the mixed numbers improper fractions so that we can then find a common denominator. To make a mixed number into an improper fraction, you multiply the denominator by the whole number and add the result to the numerator. So, for the presented data:
and
Now, to find out how many total pounds of vegetables Steven purchased, we need to add these two improper fractions together:
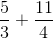
To add these fractions, they need to have a common denominator. We can adjust each fraction to have a common denominator of 
To multiply fractions, just multiply across:
We can now add the numerators together; the denominator will stay the same:
Since all of the answer choices are mixed numbers, we now need to change our improper fraction answer into a mixed number answer. We can do this by dividing the numerator by the denominator and leaving the remainder as the numerator:
This means that our final answer is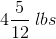 
All ACT Math Resources
