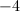Call Now to Set Up Tutoring:

(888) 888-0446

ACT Math : How to find out when an equation has no solution

Study concepts, example questions & explanations for ACT Math

Create An Account

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #131 : Equations / Inequalities

Given the following system, find the solution:

x = y – 2

2x – 2y = 2

Possible Answers:

(1, 1)

no solution

(1, 2)

(0, 1)

(0, 0)

Correct answer:

no solution

Explanation:

When 2 equations in a system have the same slopes, they will either have no solution or infinite solutions. Since the y-intercepts are not the same, there is no solution to this system.

Report an Error

Example Question #1 : How To Find Out When An Equation Has No Solution

Solve for :

27x-32=-(-27x+27)

Possible Answers:

Infinite Solutions

1.1

No solution

$-9.25\cdot 10^{-2}$

Correct answer:

No solution

Explanation:

27x-32=-(-27x+27)

Like other "solve for x" problems, to begin it, the goal is to get x by itself on one side of the equals sign. In this problem, before doing so, the imaginary -1 in front of (-27x+27) must be distributed.

27x-32=27x-27

Once this is done, you may start to try to get x by itself.

${\color{Red} 27x}-32={\color{Red} 27x}-27$

However, when subtracting 27x from either side and doing the same on the other, the 27x term cancels out. As a result, the equation becomes:

-32=-27

We know this is an untrue statement because these numbers are 5 spaces away from each other on the number line. The final answer is No Solution.

$-32\neq-27$

Report an Error

Example Question #2 : How To Find Out When An Equation Has No Solution

Given the following system, find the solution:

y = 2x + 3

3y - 5 = 6x

Possible Answers:

$\left (0, \frac{5}{3} \right )$

$\left (- \frac{2}{3}, 0 \right )$

$\left (- \frac{5}{6}, 0 \right )$

No solution

(0, 3)

Correct answer:

No solution

Explanation:

When two equations have the same slope, they will have either no solution or infinite solutions. By putting both equations into the form y = mx +b , we get:

y = 2x + 3

and

$y = 2x +\frac{5}{3}$

With the equations in this form, we can see that they have the same slope, but different y-intercepts. Therefore, there is no solution to this system.

Report an Error

Example Question #3 : How To Find Out When An Equation Has No Solution

Solve the following equation for :

$2\left ( x - 4\right ) = \frac{4x + 5}{2}$

Possible Answers:

No solution

$-\frac{3}{2}$

$\frac{13}{2}$

Infinite solutions

Correct answer:

No solution

Explanation:

In order to solve for , we must get by itself on one side of the equation.

$2\left ( x - 4\right ) = \frac{4x + 5}{2}$

First, we can distribute the on the left side of the equal sign and the $\frac{1}{2}$ on the right side.

$2x - 8= 2x +\frac{ 5}{2}$

When we try to get by itself, the terms on each side of the equation cancel out, leaving us with:

$- 8= \frac{ 5}{2}$

We know this is an untrue statement, so there is no solution to this equation.

Report an Error

Example Question #132 : Linear / Rational / Variable Equations

Find the solution to the following equation if x = 3:

y = (4x² - 2)/(9 - x²)

Possible Answers:

no possible solution

Correct answer:

no possible solution

Explanation:

Substituting 3 in for x, you will get 0 in the denominator of the fraction. It is not possible to have 0 be the denominator for a fraction so there is no possible solution to this equation.

Report an Error

Example Question #133 : Linear / Rational / Variable Equations

Nosol1

Possible Answers:

–3

There is no solution

–1/2

Correct answer:

There is no solution

Explanation:

Nosol2

Report an Error

Example Question #134 : Linear / Rational / Variable Equations

$\small h\left ( x\right )=\frac{28}{x+4}$

$\small \textup{For which of the following values of}\,x\,\textup{is the above function undefined?}$

Possible Answers:

$\small -4$

$\small 28$

None of the other answers

$\small 0$

$\small 4$

Correct answer:

$\small -4$

Explanation:

A fraction is considered undefined when the denominator equals 0. Set the denominator equal to zero and solve for the variable.

$\small x+4=0$

$\small x=-4$

Report an Error

Example Question #26 : Linear / Rational / Variable Equations

$\frac{x+2}{3}=\frac{x}{3}$ Solve for .

Possible Answers:

No solutions.

Correct answer:

No solutions.

Explanation:

Cross multiplying leaves 3x+6=3x , which is not possible.

Report an Error

Example Question #2 : How To Find Out When An Equation Has No Solution

Undefined_denom3

I. x = 0

II. x = –1

III. x = 1

Possible Answers:

I, II, and III

I only

III only

II only

II and III only

Correct answer:

I only

Explanation:

Undefined_denom2

Report an Error

Example Question #4 : How To Find Out When An Equation Has No Solution

Solve:

3(2x - 6) + 2x = 7x - 12

Possible Answers:

Correct answer:

Explanation:

First, distribute, making sure to watch for negatives.

3(2x - 6) + 2x = 7x - 12

6x - 18 + 2x = 7x - 12

Combine like terms.

8x - 18 = 7x - 12

Subtract 7x from both sides.

x - 18 = -12

Add 18 on both sides and be careful adding integers.

x = 6

Report an Error

View ACT Math Tutors

Anne
Certified Tutor

University of Maryland-Baltimore, Doctor of Science, Accounting.

View ACT Math Tutors

Satweka
Certified Tutor

The University of Texas at Dallas, Master of Science, Biomedical Engineering.

View ACT Math Tutors

Leonard
Certified Tutor

Florida State University, Bachelor of Science, Environmental Science.

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

ACT Math Tutors in Top Cities:

Atlanta ACT Math Tutors, Austin ACT Math Tutors, Boston ACT Math Tutors, Chicago ACT Math Tutors, Dallas Fort Worth ACT Math Tutors, Denver ACT Math Tutors, Houston ACT Math Tutors, Kansas City ACT Math Tutors, Los Angeles ACT Math Tutors, Miami ACT Math Tutors, New York City ACT Math Tutors, Philadelphia ACT Math Tutors, Phoenix ACT Math Tutors, San Diego ACT Math Tutors, San Francisco-Bay Area ACT Math Tutors, Seattle ACT Math Tutors, St. Louis ACT Math Tutors, Tucson ACT Math Tutors, Washington DC ACT Math Tutors

Popular Courses & Classes

GRE Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in New York City, LSAT Courses & Classes in Miami, ACT Courses & Classes in Houston, Spanish Courses & Classes in Philadelphia, SAT Courses & Classes in Boston, ISEE Courses & Classes in Houston, LSAT Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in San Diego

Popular Test Prep

ACT Test Prep in Houston, ISEE Test Prep in Washington DC, SSAT Test Prep in Seattle, SSAT Test Prep in Phoenix, SAT Test Prep in Atlanta, LSAT Test Prep in Seattle, GRE Test Prep in Dallas Fort Worth, ISEE Test Prep in Houston, SSAT Test Prep in Boston, GMAT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ACT Math : How to find out when an equation has no solution

Study concepts, example questions & explanations for ACT Math

All ACT Math Resources

Example Questions

Example Question #131 : Equations / Inequalities

Example Question #1 : How To Find Out When An Equation Has No Solution

Example Question #2 : How To Find Out When An Equation Has No Solution

Example Question #3 : How To Find Out When An Equation Has No Solution

Example Question #132 : Linear / Rational / Variable Equations

Example Question #133 : Linear / Rational / Variable Equations

Example Question #134 : Linear / Rational / Variable Equations

Example Question #26 : Linear / Rational / Variable Equations

Example Question #2 : How To Find Out When An Equation Has No Solution

Example Question #4 : How To Find Out When An Equation Has No Solution

All ACT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: