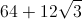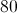Call Now to Set Up Tutoring:

(888) 888-0446

ACT Math : How to find the perimeter of a parallelogram

Study concepts, example questions & explanations for ACT Math

Create An Account

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #171 : Plane Geometry

A parallelogram, with dimensions in cm, is shown below. Act1

What is the perimeter of the parallelogram, in cm?

Possible Answers:

$64+12\sqrt{3}$

Correct answer:

$64+12\sqrt{3}$

Explanation:

The triangle on the left side of the figure has a $30^{\circ}$ and a $90^{\circ}$ angle. Since all of the angles of a triangle must add up to $180^{\circ}$ , we can find the angle measure of the third angle:

30+90=120

$180-120=60^{\circ}$

Our third angle is $60^{\circ}$ and we have a 30-60-90 triangle.

A 30-60-90 triangle has sides that are in the corresponding ratio of $x-x\sqrt{3}-2x$ . In this case, the side opposite our $30^{\circ}$ angle is , so

x=6

We also now know that

$x\sqrt{3}=6\sqrt{3}$

2x=12

Now we know all of our missing side lengths. The right and left side of the parallelogram will each be . The bottom and top will each be $20+6\sqrt{3}$ . Let's combine them to find the perimeter:

Perimeter=2w+2l

$2\cdot (12)+2\cdot (20+6\sqrt{3})$

$24+40+12\sqrt{3}$

$64+12\sqrt{3}$

Report an Error

Example Question #1 : How To Find The Perimeter Of A Parallelogram

Parallelogram2

Note: Figure NOT drawn to scale.

Give the perimeter of Parallelogram ABCD in the above diagram.

Possible Answers:

$15 + 15\sqrt{2}$

$15 + 15\sqrt{3}$

$30 \sqrt{2}$

$30 \sqrt{3}$

Correct answer:

$30 \sqrt{3}$

Explanation:

By the 30-60-90 Theorem, the length of the short leg of $\bigtriangleup BDC$ is the length of the long leg divided by $\sqrt{3}$ , so

$CD = \frac{BD}{\sqrt{3}} = \frac{15}{\sqrt{3}} = \frac{15\cdot \sqrt{3}}{\sqrt{3}\cdot \sqrt{3}}= \frac{15 \sqrt{3}}{3} = 5\sqrt{3}$

Its hypotenuse has twice the length of the short leg, so

$BC = 2 \cdot CD = 2 \cdot 5\sqrt{3}= 10 \sqrt{3}$

The perimeter of the parallelogram is

AB + BC + CD + DA

=CD + BC + CD + BC

$=5 \sqrt{3} + 10\sqrt{3} + 5 \sqrt{3} + 10\sqrt{3} = 30 \sqrt{3}$

Report an Error

Example Question #331 : Act Math

Parallelogram1

Note: Figure NOT drawn to scale.

Give the perimeter of Parallelogram ABCD in the above diagram.

Possible Answers:

$68 \sqrt{2}$

$34 + 34 \sqrt{3}$

$34 + 34 \sqrt{2}$

$68 \sqrt{3}$

Correct answer:

$34 + 34 \sqrt{2}$

Explanation:

By the 45-45-90 Theorem, the lengths of the legs of $\bigtriangleup BDC$ are equal, so

CD = BD = 17

Its hypotenuse has measure $\sqrt{2}$ that of the common measure of its legs, so

$BC = CD \cdot \sqrt{2} = 17 \sqrt{2}$

The perimeter of the parallelogram is

AB + BC + CD + DA

=CD + BC + CD + BC

$=17+ 17 \sqrt{2}+ 17 + 17\sqrt{2}= 34 + 34 \sqrt{2}$

Report an Error

Example Question #2 : How To Find The Perimeter Of A Parallelogram

Parallelogram

Note: Figure NOT drawn to scale.

To the nearest tenth, give the perimeter of Parallelogram ABCD in the above diagram.

Possible Answers:

31.4

28.3

69.4

34.7

56.7

Correct answer:

31.4

Explanation:

$\frac{BD}{CD} = \tan 65^{\circ}$

$\frac{CD}{BD} = \frac{1}{\tan 65^{\circ}}$

$CD= \frac{BD}{\tan 65^{\circ}} \approx \frac{10}{2.1445} \approx 4.66$

$\frac{BD}{BC} = \sin 65^{\circ}$

$\frac{BC}{BD} = \frac{1}{\sin 65^{\circ}}$

$BC= \frac{BD}{\sin 65^{\circ}} \approx \frac{10}{0.9063} \approx 11.03$

The perimeter of the parallelogram is

AB + BC + CD + DA

=CD + BC + CD + BC

$\approx 4.66 + 11.03 + 4.66 + 11.03 \approx 31.4$

Report an Error

Example Question #333 : Act Math

Parallelogram1

In the above figure, Parallelogram ABCD has area 100. To the nearest tenth, what is its perimeter?

Possible Answers:

45.6

47.6

50.5

48.3

54.6

Correct answer:

48.3

Explanation:

By the 45-45-90 Theorem, BD = CD . Since and are its base and height:

$A = BD \cdot CD$

$100 = CD \cdot CD = \left (CD \right ) ^{2}$

CD =10

Also by the 45-45-90 Theorem,

$BC = CD \cdot \sqrt{2} = 10 \cdot 1.4142 \approx 14.14$

The perimeter of the parallelogram is

AB + BC + CD + DA

=CD + BC + CD + BC

$\approx 10+ 14.14 + 10 + 14.14$

$\approx 48.3$

Report an Error

Example Question #334 : Act Math

Parallelogram2

In the above figure, Parallelogram ABCD has area 100. To the nearest tenth, what is its perimeter?

Possible Answers:

50.5

54.6

47.6

45.6

48.3

Correct answer:

45.6

Explanation:

By the 30-60-90 Theorem,

$BD = CD\cdot \sqrt{3}$

The area of the parallelogram is the product of height and base , so

$A = BD \cdot CD$

$100 = CD\cdot \sqrt{3}\cdot CD$

$100 = \left (CD\right )^{2} \sqrt{3}$

$\left (CD\right )^{2} = \frac{100 }{\sqrt{3}}$

$\left (CD\right )^{2} \approx \frac{100 }{1.7321}$

$\left (CD\right )^{2} \approx 57.73$

$CD \approx \sqrt{57.73} \approx 7.60$

Also by the 30-60-90 Theorem,

$BD =2\cdot CD \approx 2 \cdot 7.60 = 15.20$

The perimeter of the parallelogram is

AB + BC + CD + DA

=CD + BC + CD + BC

$\approx 7.60 + 15.20 + 7.60 + 15.20 \approx 45.6$

Report an Error

Example Question #335 : Act Math

Parallelogram

Note: Figure NOT drawn to scale.

In the above figure, Parallelogram ABCD has area 100. To the nearest tenth, what is its perimeter?

Possible Answers:

28.7

70.7

44.2

46.0

46.6

Correct answer:

46.0

Explanation:

$\frac{BD}{CD} = \tan 65^{\circ}$

$BD=CD \cdot \tan 65^{\circ}$

The area of the parallelogram is the product of height and base , so

$A = BD \cdot CD$

$100 = CD \cdot \tan 65^{\circ}\cdot CD$

$(CD)^{2} \cdot \tan 65^{\circ} = 100$

$(CD)^{2} = \frac{100}{\tan 65^{\circ} } = \frac{100}{2.1445} \approx 46.63$

$CD \approx \sqrt{46.63} \approx 6.83$

$\frac{CD}{BC} = \cos 65^{\circ}$

$\frac{BC} {CD}= \frac {1}{ \cos 65^{\circ}}$

$BC = \frac{CD}{ \cos 65^{\circ}}$

$BC \approx \frac{6.83}{0.4226} \approx 16.16$

The perimeter of the parallelogram is

AB + BC + CD + DA

=CD + BC + CD + BC

$\approx 6.83 + 16.16 + 6.83 +16.16$

$\approx 46.0$

Report an Error

View ACT Math Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

View ACT Math Tutors

Solomon
Certified Tutor

Yale University, Bachelor in Arts, Economics.

View ACT Math Tutors

Joy
Certified Tutor

Boston University, Bachelor in Arts, Conservation Biology.

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

ACT Math Tutors in Top Cities:

Atlanta ACT Math Tutors, Austin ACT Math Tutors, Boston ACT Math Tutors, Chicago ACT Math Tutors, Dallas Fort Worth ACT Math Tutors, Denver ACT Math Tutors, Houston ACT Math Tutors, Kansas City ACT Math Tutors, Los Angeles ACT Math Tutors, Miami ACT Math Tutors, New York City ACT Math Tutors, Philadelphia ACT Math Tutors, Phoenix ACT Math Tutors, San Diego ACT Math Tutors, San Francisco-Bay Area ACT Math Tutors, Seattle ACT Math Tutors, St. Louis ACT Math Tutors, Tucson ACT Math Tutors, Washington DC ACT Math Tutors

Popular Courses & Classes

GRE Courses & Classes in Seattle, GMAT Courses & Classes in New York City, ACT Courses & Classes in Dallas Fort Worth, Spanish Courses & Classes in Los Angeles, Spanish Courses & Classes in Chicago, Spanish Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Boston, LSAT Courses & Classes in Boston, ACT Courses & Classes in Miami, ACT Courses & Classes in Atlanta

Popular Test Prep

ACT Test Prep in Atlanta, LSAT Test Prep in Houston, SAT Test Prep in Denver, LSAT Test Prep in Philadelphia, ISEE Test Prep in San Diego, ISEE Test Prep in Miami, GRE Test Prep in Chicago, LSAT Test Prep in Miami, SAT Test Prep in Houston, SSAT Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ACT Math : How to find the perimeter of a parallelogram

Study concepts, example questions & explanations for ACT Math

All ACT Math Resources

Example Questions

Example Question #171 : Plane Geometry

Example Question #1 : How To Find The Perimeter Of A Parallelogram

Example Question #331 : Act Math

Example Question #2 : How To Find The Perimeter Of A Parallelogram

Example Question #333 : Act Math

Example Question #334 : Act Math

Example Question #335 : Act Math

All ACT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: