All Advanced Geometry Resources
Example Questions
Example Question #1 : How To Find The Length Of The Diagonal Of A Kite
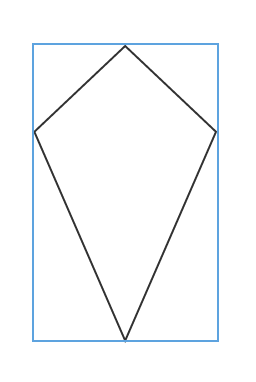
The area of the rectangle is 
The area of a kite is half the product of the diagonals.
The diagonals of the kite are the height and width of the rectangle it is superimposed in, and we know that because the area of a rectangle is base times height.
Therefore our equation becomes:

We also know the area of the rectangle is 
Thus,, the area of the kite is 
Example Question #1 : How To Find The Length Of The Diagonal Of A Kite
Given: Quadrilateral 





Give the length of diagonal 
None of the other responses is correct.
The Quadrilateral 


. We call the point of intersection 

The diagonals of a quadrilateral with two pairs of adjacent congruent sides - a kite - are perpendicular; also, 







By the 30-60-90 Theorem, since 


By the 45-45-90 Theorem, since 


The diagonal 

Example Question #1 : How To Find The Length Of The Diagonal Of A Kite

Using the kite shown above, find the length of the red (vertical) diagonal.
In order to solve this problem, first observe that the red diagonal line divides the kite into two triangles that each have side lengths of 



The solution is:
Example Question #2 : How To Find The Length Of The Diagonal Of A Kite
A kite has two perpendicular interior diagonals. One diagonal is twice the length of the other diagonal. The total area of the kite is 
To solve this problem, apply the formula for finding the area of a kite:
However, in this problem the question only provides information regarding the exact area. The lengths of the diagonals are represented as a ratio, where
Therefore, it is necessary to plug the provided information into the area formula. Diagonal 


The solution is:
Thus, if 

Example Question #3 : How To Find The Length Of The Diagonal Of A Kite
A kite has two perpendicular interior diagonals. One diagonal has a measurement of 

This problem can be solved by applying the area formula:
Since this question provides the area of the kite and length of one diagonal, plug that information into the equation to solve for the missing diagonal.
Thus the solution is:
Example Question #6 : Kites
A kite has two perpendicular interior diagonals. One diagonal has a measurement of 

This problem can be solved by applying the area formula:
Since this question provides the area of the kite and length of one diagonal, plug that information into the equation to solve for the missing diagonal.
Thus the solution is:
Example Question #1 : How To Find The Length Of The Diagonal Of A Kite
A kite has two perpendicular interior diagonals. One diagonal has a measurement of 

First find the length of the missing diagonal before you can find the sum of the two perpendicular diagonals.
To find the missing diagonal, apply the area formula:
This question provides the area of the kite and length of one diagonal, plug that information into the equation to solve for the missing diagonal.
Therefore, the sum of the two diagonals is:
Example Question #1 : How To Find The Length Of The Diagonal Of A Kite
A kite has two perpendicular interior diagonals. One diagonal has a measurement of 

You must find the length of the missing diagonal before you can find the sum of the two perpendicular diagonals.
To find the missing diagonal, apply the area formula:
This question provides the area of the kite and length of one diagonal, plug that information into the equation to solve for the missing diagonal.
Therefore, the sum of the two diagonals is:
Example Question #21 : Quadrilaterals

The area of the kite shown above is 

To find the length of the black diagonal apply the area formula:
Since this question provides the area of the kite and length of one diagonal, plug that information into the equation to solve for the missing diagonal.
Thus the solution is:
Example Question #10 : Kites
A kite has two perpendicular interior diagonals. One diagonal has a measurement of 

This problem can be solved by applying the area formula:
Since this question provides the area of the kite and length of one diagonal, plug that information into the equation to solve for the missing diagonal.
Thus the solution is:
All Advanced Geometry Resources






























































































