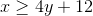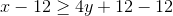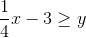All Algebra 1 Resources
Example Questions
Example Question #1 : How To Graph A Two Step Inequality
Which graph depicts the following inequality?
Possible Answers:




No real solution.
Correct answer:

Explanation:
Let's put the inequality in slope-intercept form to make it easier to graph:
The inequality is now in slope-intercept form. Graph a line with slope 

Because the inequality sign is greater than or equal to, a solid line should be used.
Next, test a point. The origin 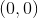
The statement is false. Therefore, the section of the graph that does not contain the origin should be shaded.
All Algebra 1 Resources
Popular Subjects
GRE Tutors in Los Angeles, Calculus Tutors in Dallas Fort Worth, GMAT Tutors in New York City, ACT Tutors in Miami, Algebra Tutors in Miami, MCAT Tutors in Atlanta, ISEE Tutors in Boston, MCAT Tutors in Denver, GRE Tutors in Phoenix, ISEE Tutors in Philadelphia
Popular Courses & Classes
SSAT Courses & Classes in San Diego, Spanish Courses & Classes in Philadelphia, SAT Courses & Classes in Miami, SSAT Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Chicago, Spanish Courses & Classes in Miami, Spanish Courses & Classes in Chicago, LSAT Courses & Classes in New York City, GMAT Courses & Classes in Boston
Popular Test Prep
GRE Test Prep in New York City, LSAT Test Prep in New York City, MCAT Test Prep in Boston, GRE Test Prep in Boston, SAT Test Prep in Los Angeles, ISEE Test Prep in San Francisco-Bay Area, LSAT Test Prep in San Francisco-Bay Area, MCAT Test Prep in Denver, ACT Test Prep in Seattle, GRE Test Prep in San Diego