All AP Physics 1 Resources
Example Questions
Example Question #1 : Impulse And Momentum
In a billiards game, one player hits the cue ball towards another ball. The cue ball has a mass of 0.1kg and hits the other ball with a velocity of 

Since the collision is completely elastic, we know that both momentum and kinetic energy are conserved. We can write the following equations (initial momentum and energy of the second ball are neglected since it is not moving:
Rearrange the first equation for 

We can rewrite the second equation as:
Substitute our equation for 
Rearranging, we get:
Plug in our values for the initial and final velocities:
To solve for mass, we'll use our earlier expression for 
Example Question #2 : Impulse And Momentum
Two sumo wrestlers are in a match. At the start of the match, they both lunge at each other. They hit and miraculously come to a stand still. One wrestler was 200kg and traveling at a velocity of 

It does not matter whether the collision is elastic or inelastic (although it would be best to assume that it's inelastic). Momentum is conserved in either type of collision, and is the only value needed for our calculation. Since they come to a standstill, their momentums at the moment of collision are equal and opposite:
Rearrange to solve for 
Plug in the given values from the question and solve:
Example Question #1 : Impulse And Momentum
One car with a mass of 400kg is traveling east at 

Since the collision is completely inelastic, momentum is conserved but energy is not. Furthermore, the two cars stick to each other and travel as one. The equation for conservation of momentum is as follows:
There are two inital masses with different velocities and one final mass with a single velocity. Therefore, we can write:
Rearranging for final velocity, we get:
At this point, we can denote which direction is positive and which is negative. Since the car traveling west has more momentum, we will consider west to be positive. Substituting our values into the equation, we get:
Since this value is positive, the final answer is 
Example Question #461 : Ap Physics 1
A marble of mass 

Impulse can be written as either of two popular expressions:
From the problem statement, we can determine the velocity of the marble as it hits the floor, allowing us to use the latter expression. To determining the velocity of the marble, we can use the equation for conservation of energy:
Assuming the final height is zero, we can eliminate initial kinetic energy and final potential energy. Therefore, we can write:
Canceling out mass and rearranging for final velocity, we get:
We know these variables, allowing us to solve for the velocity:
Plugging this value into the expression for impulse, we get:
Example Question #1 : Impulse And Momentum
Consider the following system:
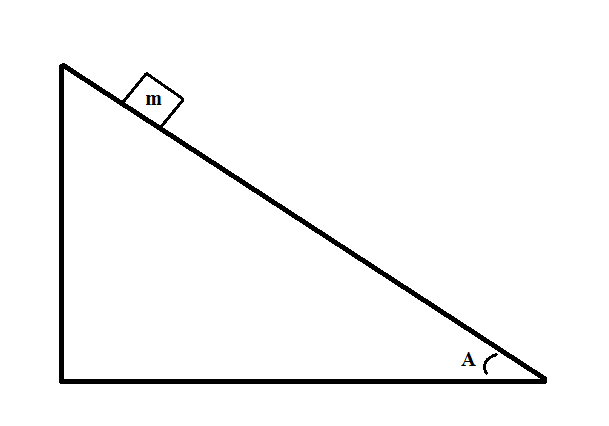
If the block has a mass of 


To calculate the momentum of the block, we first need to know the velocity of the block. This can be found using the equation for the conservation of momentum:
If we assume that the final height is zero, we can eliminate initial kinetic energy and final potential energy, getting:
Substituting expressions for each term, we get:
Cancel out mass and rearrange to solve for velocity:
We can use the horizontal distance traveled and the angle of the slope to determine the initial height:
Now that we have the initial height, we can solve for final velocity:
Finally, we can now use the equation for momentum to solve the problem:
Example Question #1 : Impulse And Momentum
Two astronauts in space are traveling directly towards each other. Astronaut A has a mass of 



Momentum is always conserved. Equation for conservation of momentum:
There is only one velocity on the right since the two astronauts grab onto each other, thus they move together at the same velocity. Solve.
Example Question #7 : Impulse And Momentum
A 


The equation for momentum is:
To maintain conservation of momentum, a new state must have the same momentum as a previous state:
Since the rock and the bean bag move together after the collision, 
Plug in known values and solve.
Example Question #8 : Impulse And Momentum
A 150g baseball is thrown with a speed of 
To solve this problem, we need to consider the change in the ball's momentum. To do so, we'll use the following equation.
Rearrange the above equation to solve for the average force.
Example Question #9 : Impulse And Momentum
Joe, of mass 90kg, jumps straight up. To do so, he bends his knees and produces an upwards force that results in a constant upward net force of 100N. If Joe experiences this force for 0.9s before leaving the ground, what is Joe's velocity immediately after he leaves the ground?
To solve this problem we need to use the relationship between force and impulse, which is given by the following equation:
This equation represents that the rate of change of momentum with respect to time is equal to the net force that causes said change in momentum. Thus:
Note that Joe must have an initial velocity of 
Solve for 
Example Question #10 : Impulse And Momentum
Which of the following explains why when we land on our feet, we instinctively bend our knees? Hint: think about the relationship between force, impulse, and time.
By bending our knees we extend the time it takes us to stop, which increases the impact force
By bending our knees we extend the time it takes us to stop, which diminishes the impact force
When we bend our knees we extend the time in which we apply the force that stops us, so our impulse is greater
When we bend our knees we extend the time in which we apply the force that stops us, so our impulse is smaller
By bending our knees we use a greater force to stop, which makes the impulse smaller
By bending our knees we extend the time it takes us to stop, which diminishes the impact force
Say that, when we hit the ground, we have a velocity 

Note that the initial momentum does not depend on the impact force nor on how much time it takes to stop. The initial momentum depends on the velocity we have when we first hit the ground. This velocity is given by whatever happened before we hit the ground, which no longer concerns us since we only care about what happens from the moment we first hit the ground till the moment we stop. Yes, the time that passes for you to stop is very small, but it is impossible for it to be zero. So we have that the change in momentum (impulse) is a constant:


Remember that any change in momentum for a given mass occurs because its velocity changes. The velocity of the mass changes due to an acceleration and an acceleration is caused by a force. This gives us a relationship between force and impulse:
In our scenario, 




Certified Tutor
All AP Physics 1 Resources










































































































